Maths de terminale : exercice de logarithme népérien et intégrale. Fonction, logarithme, exponentielle, inégalité, variation, asymptote.
Exercice N°460 :
Soit f la fonction définie sur [0 ; +∞[ par :
f(x) = x + ln(1 + e-x).
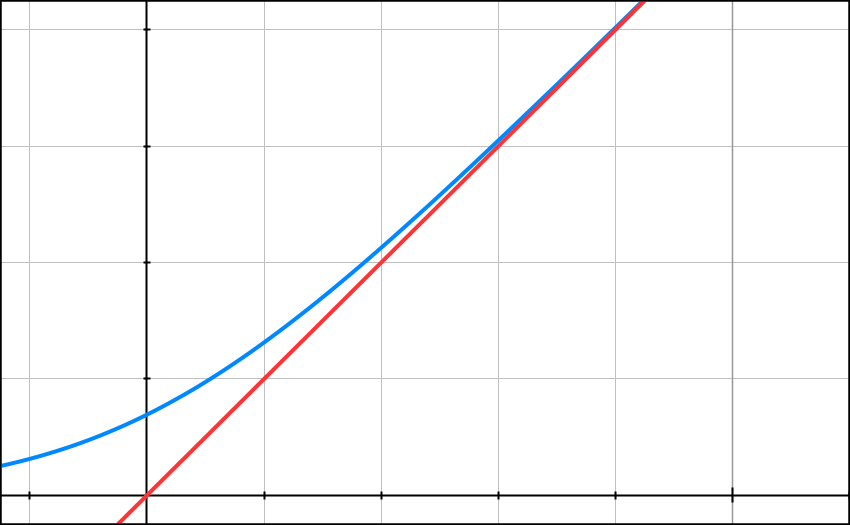
Sa courbe représentative (C) ainsi que la droite (D) d’équation
y = x
sont données ci-dessous dans un repère orthonormal d’unité graphique 2 cm.
1) Montrer que f est croissante et positive sur [0 ; +∞[.
2) Montrer que la courbe (C) admet pour asymptote la droite (D).
3) Étudier la position de (C) par rapport à (D).
Soit I l’intégrale définie par :
I = ∫[de 0 à 1] ln(1 + e-x) dx = ∫[de 0 à 1] [f(x) – x] dx.
On ne cherchera pas à calculer I.
4) Donner une interprétation géométrique de I.
5) Montrer que pour tout réel t ≥ 0,
on a ln (1 + t) ≤ t.
(On pourra étudier les variations de la fonction g définie sur [0 ; +∞[
par g(t) = ln(1 + t) – t.)
Dans la suite, on admettra que pour tout réel t ≥ 0,
t/(t+1) ≤ ln (1 + t).
6) En déduire que pour tout x de [0 ; +∞[, on a :
e-x/(e-x + 1) ≤ ln(1 + e-x) ≤ e-x.
7) Montrer que
ln( 2/(1 + e-1) ) ≤ I ≤ 1 – e-1.
8) En déduire un encadrement de I d’amplitude 0,4 par deux nombres décimaux.
Question “trace de recherche” :
On désigne par M et N les points de même abscisse x appartenant respectivement à (C) et (D). (D) est la droite du graphique en haut et (C) est la courbe.
On juge que M et N sont indiscernables sur le graphique lorsque la distance MN est inférieure à 0.5 mm.
9) Déterminer l’ensemble des valeurs de x pour lesquelles M et N sont indiscernables.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, logarithme népérien, intégrale.
Exercice précédent : Primitives – Exponentielle, suite, algorithme, limite – Terminale

