Exercice de maths de terminale sur les probabilités avec algorithme, loi uniforme, exponentielle, tableau, loi, fonction de densité.
Exercice N°454 :
On admet que l’on puisse assimiler la fonction « random » d’une calculatrice à une variable aléatoire suivant une loi uniforme sur [0 ; 1].
Soit p un nombre réel appartenant à [0 ; 1].
1) Calculer P(random ≤ p).
On considère l’algorithme ci-dessous :

2) Quelle est la loi de la variable aléatoire X simulée par cet algorithme ? Compléter le tableau suivant :

3) Modifier l’algorithme pour qu’il affiche une valeur prise par une variable aléatoire suivant une loi binomiale de paramètres n et p qui seront entrés par l’utilisateur.
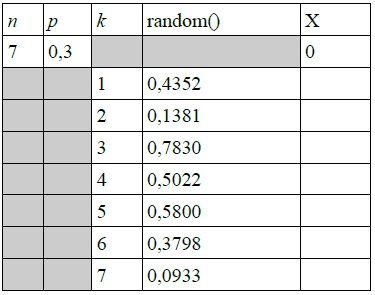
4) Complétez le tableau suivant qui décrit l’exécution pas à pas de l’algorithme dans un cas particulier où n = 7, p = 0.3 et où on suppose obtenues les 7 valeurs indiquées pour random() (arrondies à 10−4).
Autre chose, la durée de vie, en heures, des ampoules fluo-compactes est une variable aléatoire T qui suit une loi exponentielle d’espérance 10000.
5) Donner la fonction densité de probabilité de cette variable aléatoire T.
6) Calculer P(T ≤ 8000). Que signifie ce calcul ?
7) Sachant qu’une ampoule a déjà fonctionné pendant 7000 heurs, quelle est la probabilité que sa durée de vie dépasse 12000 heures ?
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : algorithme, loi uniforme, exponentielle.
Exercice précédent : Lois continues – Normale, fluctuation, échantillon – Terminale S

