Exercice de maths sur le calcul d’intégrale et de primitive de terminale. Fonctions de demande et d’offre, point d’équilibre, valeur moyenne.

Exercice N°472 :

Primitive, fonction, demande, offre, calculs, moyenne, terminale

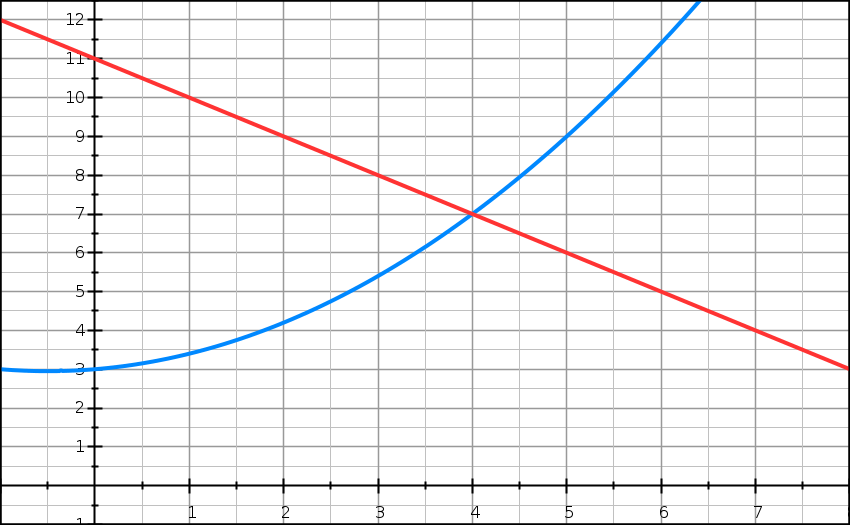
La fonction d’offre d’un bien est définie sur [0 ; 10] par :
f(x) = 0.2x2 + 0,2x + 3 où x est la quantité en tonnes et f(x)
est le prix unitaire en milliers d’euros par tonne.
La fonction de demande de ce bien est définie sur [0 ; 10] par :
g(x) = 11 – x.
Les courbes de f et g sont tracées dans le repère ci-dessus.

1) Résoudre f(x) = g(x) et en déduire la quantité d’équilibre qE, notée et le prix d’équilibre notée pE. Lis la suite »

Ecris le premier commentaire

Exercice de maths de terminale sur primitive et intégrale, fonction rationnelle, étude de signe, aire sous la courbe, bénéfice, moyenne.

Exercice N°471 :

Primitives, rationnelle, signe, intégrale, bénéfice, terminale

On considère la fonction définie sur [3 ; 10] par
f(x) = (x2 – 2x – 8)/(x – 1)2.
On donne ci-dessus sa courbe Cf dans un repère orthogonal d’unités graphiques : 2 cm en abscisses et 5 cm en ordonnées.

1) Déterminer par calcul le signe de f(x) sur [3 ; 10]. Lis la suite »

Ecris le premier commentaire

Exercice de maths de terminale sur qcm, primitives et intégrales avec études de courbes, pente, tangente, aire sous la courbe

Exercice N°470 :

Primitives, intégrales, courbes, dérivée, aire, pente, terminale

Exercice N°470 :

QCM avec une seule bonne réponse possible par question :

Pour les questions 1) à 6), on considère la fonction f définie et dérivable sur
[-2 ; 4] représentée par la courbe C et la g fonction définie et dérivable sur
[-2 ; 4] représentée par la courbe Γ Les points notés par une croix sont des
points connus de ces courbes. La droite T est la tangente à la courbe C de au
point d’abscisse 0.

Primitives, intégrales, courbes, dérivée, aire, pente, terminale

1) Laquelle de ces phrases est vraie ? Lis la suite »

Ecris le premier commentaire

Maths de terminale : exercice sur le logarithme népérien avec continuité, tangente, limite, variation, fonction, équation, solution unique.

Exercice N°657 :

Exercice, logarithme, continuité, tangente, limite, variation, solution, unique, terminale, Danau Tempe, Sulawesi Selatan

Exercice N°657 :

Soit f définie sur D = R+* par
f(x) = x×ln(x) – 2x + 1.

1) Déterminer les limites de f aux bornes de D. Lis la suite »

Ecris le premier commentaire

Exercice de maths sur les primitives avec valeur moyenne d’intégrale de terminale, aire sous la courbe, intervalle, unité d’aire.

Exercice N°469 :

Primitives, intégrale, moyenne, aires, puissance, terminale

Exercice N°469 :

1) Calculer la valeur moyenne de la fonction définie sur R par
x → x3 sur l’intervalle [−m ; m] où m est un réel non nul. Lis la suite »

Ecris le premier commentaire

Exercice de maths sur la primitive, racine, exponentielle, terminale. Intégrales avec fonctions polynôme, fraction, logarithme, puissances.

Exercice N°468 :

Primitives, calculs, intégrale, racine, expo, carré, terminale

Exercice N°468 :

1) Déterminer une primitive de la fonction f définie sur ]-∞ ; 1] par
f(x) = 5/√(3 – 2x). Lis la suite »

Ecris le premier commentaire

Exercice de maths de terminale sur le logarithme népérien avec limites, équations, inéquations, fonction, second degré, tangente.

Exercice N°352 :

Logarithme népérien, limites, équations, inéquations, terminale

Exercice N°352 :

1-2-3-4) Étudier les limites aux bornes de l’intervalle I :

1) f1(x) = (ln x)4 avec I = R+*. Lis la suite »

Ecris le premier commentaire

Exercice de maths de terminale de primitive, intégrale, exponentielle, cosinus, rationnelle, sinus, inégalité, limite, encadrement, inverse.

Exercice N°425 :

Primitives, exponentielle, cosinus, rationnelle, limite, terminale

Exercice N°425 :

1-2-3-4) Calculer les intégrales suivantes :

1) ∫[de 0 à 1] e1-2x dx, Lis la suite »

Ecris le premier commentaire

Exercice de maths de terminale sur le logarithme népérien, suite, algorithme. Fonction, dérivée, variations, TVI, limite, récurrence.

Exercice N°350 :

Exercice, logarithme népérien, suite, algorithme, fonction, terminale

Exercice N°350 :

Étude d’une fonction :

On considère la fonction f définie et dérivable sur l’intervalle
[0 ; +∞[par
f(x) = 5 ln(x + 3) − x.

On appelle f ‘ la fonction dérivée de la fonction f sur [0 ; +∞[.
1) Calculer f ‘ (x) et étudier son signe sur [0 ; +∞[. Lis la suite »

Ecris le premier commentaire

Maths de terminale : exercice de logarithme népérien avec bénéfice, quotient, dérivée, variation, économie, maximum, unitaire, total.

Exercice N°423 :

Exercice, logarithme népérien, quotient, bénéfice, maximum, terminale

Exercice N°423 :

Une entreprise de sous–traitance fabrique des pièces pour l’industrie automobile. Sa production pour ce type de pièces varie de 1000 à 5000 pièces par semaine, selon la demande. On suppose que toutes les pièces produites sont vendues.
Le bénéfice unitaire, en euro, en fonction du nombre de pièces produites par semaine, est modélisé par la fonction f définie sur [1 ; 5] par :
f(x) = ( 2ln(x) + 1 )/x,
avec x exprimé en millier de pièces et f(x) exprimé en euro.

1) Montrer que, sur [1 ; 5],
f ‘ (x) = ( 1 – 2ln(x) )/x2. Lis la suite »

Ecris le premier commentaire

« Articles précédents     Articles suivants »
✕
FrenchMaths.com

GRATUIT
VOIR