Exercice de maths de terminale sur le logarithme népérien, suite, algorithme. Fonction, dérivée, variations, TVI, limite, récurrence.
Exercice N°350 :

Exercice N°350 :
Étude d’une fonction :
On considère la fonction f définie et dérivable sur l’intervalle
[0 ; +∞[par
f(x) = 5 ln(x + 3) − x.
On appelle f ‘ la fonction dérivée de la fonction f sur [0 ; +∞[.
1) Calculer f ‘ (x) et étudier son signe sur [0 ; +∞[.
2) Donner, dans un tableau, les variations de f sur l’intervalle
[0 ; +∞[.
3) Montrer que, pour tout x strictement positif on a :
f(x) = x( 5[(ln x)/x] − 1 ) + 5ln ( 1 + [3/x] ).
4) En déduire la limite de f en +∞.
5) Compléter le tableau de variation de f sur l’intervalle [0 ; +∞[.
6) Montrer que l’équation f(x) = 0 admet une unique solution dans l’intervalle [0 ; +∞[. On notera α cette solution.
7) Après avoir vérifié que α appartient à l’intervalle [14 ; 15], donner une valeur approchée de α à 10−2 près.
8) En déduire le signe de f sur l’intervalle [0 ; +∞[.
Étude d’une suite :
Soit (un) la suite définie par :
{ u0 = 4
{ un+1 = 5 ln (un + 3) pour tout entier naturel n ≠ 0.
On considère la fonction g définie sur l’intervalle [0 ; +∞[ par
g(x) = 5 ln(x + 3).
Ci-dessous, on a tracé dans un repère orthonormé la droite D d’équation y = x et la courbe C, courbe représentative de la fonction g.
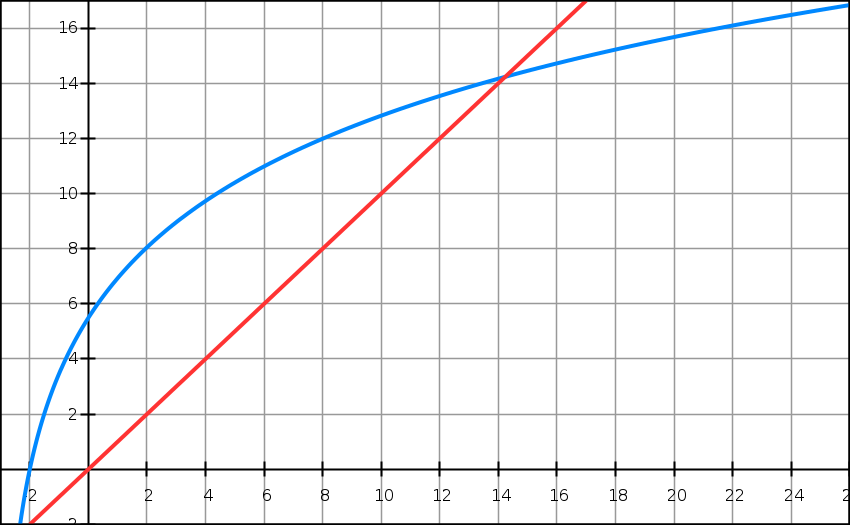
9) Construire sur l’axe des abscisses les termes u0, u1, u2 de la suite (un) en utilisant la droite et la courbe données et en laissant apparents les traits de construction.
10) Formuler une conjecture sur le sens de variations de la suite (un) et une conjecture sur sa convergence.
11) Étudier le sens de variations de la fonction g sur l’intervalle
[0 ; +∞[.
12) Vérifier que g(α) = α où α est défini dans la question 6).
13) Démontrer par récurrence que, pour tout entier naturel n, on a
0 ≤ un ≤ α.
14) Démontrer alors les deux conjectures émises à la question 10).
15) En utilisant la question 6), justifier que
limn→+∞un = α
On considère l’algorithme suivant :

16) Justifier que cet algorithme se termine.
17) Donner la valeur que cet algorithme affiche (on arrondira à 5 décimales).
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : logarithme népérien, suite, algorithme.
Exercice précédent : Algorithmique – Suite, somme, formes récurrentes – Première

