Exercice de maths sur les primitives avec valeur moyenne d’intégrale de terminale, aire sous la courbe, intervalle, unité d’aire.
Exercice N°469 :

Exercice N°469 :
1) Calculer la valeur moyenne de la fonction définie sur R par
x → x3 sur l’intervalle [−m ; m] où m est un réel non nul.
Soit g : R → R une fonction continue.
2) Calculer ∫[de 4 à 4] g(x) dx
3) Déterminer une primitive de v : x → x(x2 + 1)9.
Soit p et q deux fonctions définies sur R par
p(x) = x2 + x + 2
et
q(x) = x + 3.
On note Cp et Cq leurs courbes respectives dans un repère orthonormé.
4) Étudier la position relative des deux courbes.
5) Calculer l’aire de la surface située entre les deux courbes et délimitée
en abscisse par −1 ≤ x ≤ 1.
La courbe ci-dessous représente une fonction w définie sur [−1 ; 3].
6) Calculer l’aire en cm2 du triangle OAB.
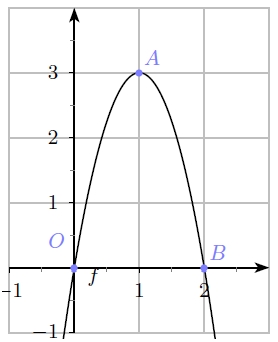
7) Expliquer pourquoi 3 ≤ ∫[de 0 à 2] w(x) dx ≤ 6.
8) Calculer la valeur moyenne de la fonction h définie par
h(x) = (x2/2) – (2/x2) – 1
sur l’intervalle [2 ; 6].
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : valeur moyenne, intégrale, terminale.
Exercice précédent : Primitives – Calculs, intégrale, racine, expo, carré – Terminale

