Exercice de maths de terminale sur le logarithme népérien, suite, algorithme. Fonction, dérivée, variations, TVI, limite, récurrence.
Exercice N°350 :
Exercice N°350 :
Étude d’une fonction :
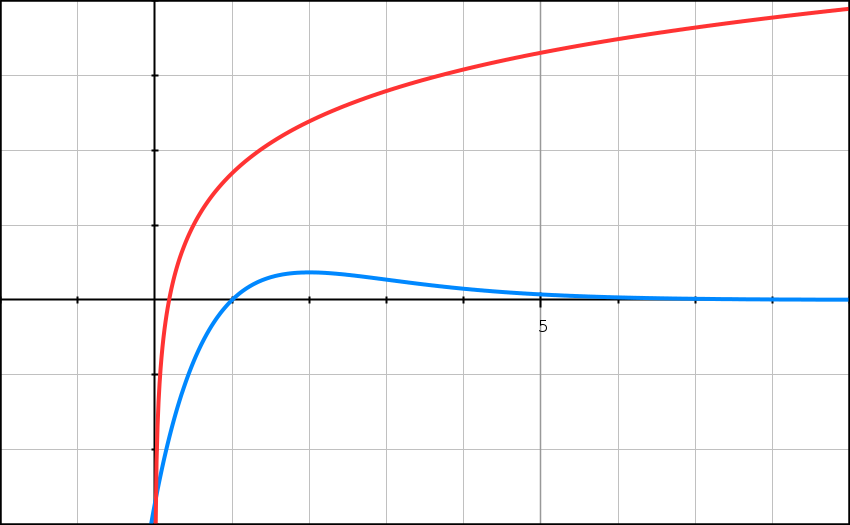
On considère la fonction f définie et dérivable sur l’intervalle
[0 ; +∞[par
f(x) = 5 ln(x + 3) − x.
On appelle f ‘ la fonction dérivée de la fonction f sur [0 ; +∞[.
1) Calculer f ‘ (x) et étudier son signe sur [0 ; +∞[. Lis la suite »
Maths de première sur les suites arithmétique et géométrique, exercice corrigé. Raison, premier terme, expressions explicites, récurrente.
Exercice N°112 :
Exercice N°112 :
Une personne loue une villa à partir du 1er janvier 2023. Elle a le choix entre deux formules de contrat. Dans les deux cas, le loyer annuel initial est de 8800 €.
Première formule :
Le locataire accepte chaque année une augmentation de 3 % du loyer de l’année précédente. On note un le montant du loyer annuel en euros de l’année (2023 + n).
On a donc u0 = 8800.
1) Calculer u1 et u2. Lis la suite »
Exercice de maths de terminale sur la primitive, exponentielle, suite, intégrale, variation, algorithme, convergence, limite, dérivation.
Exercice N°459 :
Exercice N°459 :
On considère la suite (In) définie pour n entier naturel non nul par :
In = ∫[de 0 à 1] xnex2dx.
Soit g la fonction définie par
g(x) = xex2.
1) Démontrer que la fonction G définie sur R par
G(x) = (1/2)ex2
est une primitive sur R de la fonction g. Lis la suite »
Maths de terminale : exercice d’intégrale avec suite et exponentielle. Primitive, formule, fonction, égalité et inégalité, limite.
Exercice N°463 :
Exercice N°463 :
On considère la suite (un) définie pour tout entier naturel n par :
un = ∫[de 0 à 1] e-nx/(1 + e-x) dx
1) Montrer que u0+u1 = 1. Lis la suite »
Exercice de maths de première sur les suites pour des intérêts composés avec suite auxiliaire géométrique pour trouver la suite principale.
Exercice N°007 :
Exercice N°007 :
Le premier janvier 2012, on a placé 5000 euros à intérêts composés au taux annuel de 4 % (cela signifie que les intérêts ajoutés au capital à chaque nouvelle année représentent 4 % du capital de l’année précédente).
Chaque 1er janvier, on place 200 euros supplémentaire dans ce compte.
On note C0 = 5000 le capital disponible au 1er janvier de l’année 2012, et Cn le capital disponible au premier janvier de l’année (2012 + n).
1) Calculer les valeurs exactes de C1 et C2. Lis la suite »
Maths de terminale : exercice d’intégrale, logarithme et suite. Fonction, variation, récurrence, fonction, continuité, limite, convergence.
Exercice N°458 :
Exercice N°458 :
On considère la fonction g définie sur l’intervalle [1 ; +∞[ par :
g(x) = ln(2x) + 1 − x.
Cette question demande le développement d’une certaine démarche comportant plusieurs étapes.
1) Démontrer que l’équation g(x) = 0 admet sur l’intervalle [1 ; +∞[ une unique solution notée α.
Donner un encadrement au centième de α.
2) Démontrer que ln(2α) + 1 = α. Lis la suite »
Maths de première : exercice de suite, variation, croissante, décroissante. Étude du signe d’un polynôme du second degré, affine, fraction.
Exercice N°009 :
Exercice N°009 :
Les suites un, vn et wn sont définies pour tout entier n, par :
un = 1 – 3n,
v0 = 4/9,
vn+1 = 3vn/2,
wn = n2/2n.
1) Compléter le tableau suivant : Lis la suite »
Maths de terminale : exercice sur les suite, fonction, convergence. Premier terme, récurrence, graphique, raison, limite, algorithme.
Exercice N°176 :
On considère la suite (un) définie par u0 = 0 et
un+1 = (3un + 4)/(un + 3).
On va étudier cette suite avec deux méthodes différentes.
Première méthode :
On considère la fonction f définie sur [0 ; 2] par :
f(x) = (3x + 4)/(x + 3).
1) Étudier la fonction f (variations, etc). Lis la suite »
Exercice de maths de terminale sur les probabilités, suites, arbre, récurrence, raisonnement, limite, entier minimal, calculs.
Exercice N°182 :
Exercice N°182 :
Un joueur débute un jeu vidéo et effectue plusieurs parties successives.
On admet que :
– la probabilité qu’il gagne la première partie est de 0,1.
– s’il gagne une partie, la probabilité de gagner la suivante est égale à 0,8.
– s’il perd une partie, la probabilité de gagner la suivante est égale à 0,6
On note, pour tout entier naturel n non nul :
– Gn l’événement « le joueur gagne la n-ième partie » ;
– pn la probabilité de l’vénement Gn.
On a donc p1 = 0,1.
1) Montrer que p2 = 0,62. On pourra s’aider d’un arbre pondéré. Lis la suite »
Maths de terminale : exercice de logarithme népérien avec suite, fonction exponentielle. Limites, sens de variation, convergence, auxiliaire.
Exercice N°359 :
Exercice N°359 :
Soit g la fonction définie pour tout nombre réel x de l’intervalle
]0 ; +∞[ par g(x) = x – ln(x).
1) Déterminer les limites de la fonction g en 0 et en +∞. Lis la suite »
