Maths de terminale : exercice sur les suite, fonction, convergence. Premier terme, récurrence, graphique, raison, limite, algorithme.
Exercice N°176 :
On considère la suite (un) définie par u0 = 0 et
un+1 = (3un + 4)/(un + 3).
On va étudier cette suite avec deux méthodes différentes.
Première méthode :
On considère la fonction f définie sur [0 ; 2] par :
f(x) = (3x + 4)/(x + 3).
1) Étudier la fonction f (variations, etc).
2) Montrer que : Si x ∈ [0 ; 2] alors f(x) ∈ [1 ; 2].
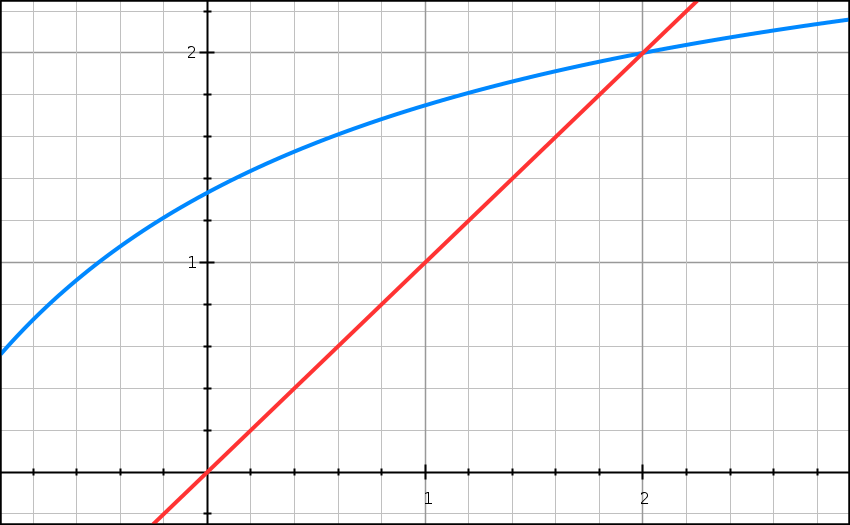
Ci-dessus, la courbe de la fonction f et la droite d’équation y = x sont tracées.
3) Construire les points A0, A1, A2, A3 d’ordonnée nulle et d’abscisses respectives u0, u1, u2, u3.
4) Que suggère le graphique concernant les sens de variation et la convergence de la suite (un) ?
5) Démontrer par récurrence que pour tout entier naturel n,
0 ≤ un ≤ un+1 ≤ 2.
6) En déduire que la suite (un) converge et déterminer sa limite l.
Passons à la seconde méthode :
On considère la suite (vn) définie pour tout entier naturel n par :
vn = (un – 2)/(un + 2).
7) Démontrer que (vn) est une suite géométrique de raison 1/5.
8) Exprimer vn en fonction de n.
9) Démontrer que pour tout entier naturel n,
un = (2 + 2vn)/(1 – vn).
10) En déduire la convergence de la suite un et la valeur de sa limite l.
Soit E un réel strictement positif.
11) Écrire un algorithme donnant le plus petit entier naturel N tel que
|uN – l| ≤ E.
12) Programmer cet algorithme à l’aide de votre calculatrice et donner la valeur de N correspondant à E = 10-12.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, suite, fonction, convergence.
Exercice précédent : Probabilités – Conditionnelles, arbre, intersection – Première

