Maths de première : exercice, exponentielle avec équations et inéquations. Fonction, produit et quotient, tableau de signe.
Exercice N°665 :
Exercice N°665 :
1-2-3) Résoudre les équations suivantes dans R :
1) e-2x = 0, Lis la suite »
Maths de première : exercice d’exponentielle avec variation et équation. Fonction produit et quotient, inéquation, inégalité.
Exercice N°664 :
Exercice N°664 :
1) Étudier les variations de la fonction f définie sur R par :
f(x) = (x2 – 3x + 1)ex. Lis la suite »
Exercice de maths de première sur la fonction et la dérivée exponentielle, tableau de variation, étude de signe, équation de tangente.
Exercice N°333 :
Exercice N°333 :
On considère la fonction f définie sur R par
f(x) = (-4x2 + 5)e-x + 3.
On note (C) la courbe représentative de la fonction f dans un repère orthogonal.
On note f ‘ la dérivée de f sur R.
1) Démontrer que pour tout réel x ∈ R,
f ‘ (x) = (4x2 – 8x – 5)e-x. Lis la suite »
Exercice de maths de terminale sur la fonction exponentielle avec calcul de dérivée, factorisation, tableaux de variation, inéquations.
Exercice N°341 :
Exercice N°341 :
On considère la fonction f définie sur R par
f(x) = 2ex – e2x.
1) Calculer la dérivée f ‘ de f. Lis la suite »
Maths : exercice sur l’exponentielle avec système et variation, valeurs intermédiaires, coût, primitive, intégrale, première, terminale.
Exercice N°335 :
Exercice N°335 :
Soit f la fonction définie sur [0 ; 5] par
f(x) = (ax + b)e−x
où a et b sont deux réels.
On note f ‘ la fonction dérivée de f.
1) Montrer que pour tout nombre réel x,
f ‘ (x) = (a − b − ax)e−x. Lis la suite »
Exercice d’exponentielle et logarithme népérien. Maths de terminale avec équation et fonction. Variations, conjecture, tvi, courbe.
Exercice N°354 :
On considère l’équation (E) d’inconnue x réelle :
ex = 3(x2 + x3).
Le graphique ci-dessous donne la courbe représentative de la fonction exponentielle et celle de la fonction f définie sur R par
f(x) = 3(x2 + x3)
telles que les affiche une calculatrice dans un même repère orthogonal.
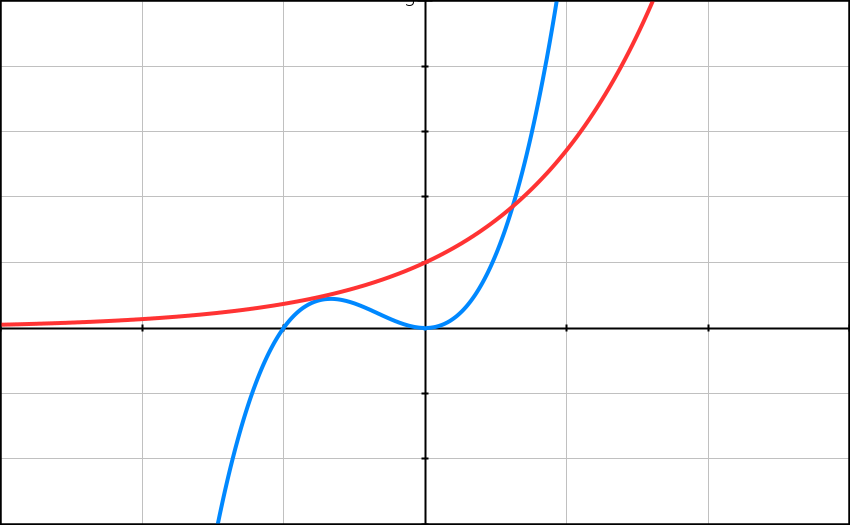
1) A l’aide du graphique ci-dessus, conjecturer le nombre de solutions de Lis la suite »
Maths de terminale : exercice d’exponentielle avec fonction auxiliaire. Continuité, étude de signe, dérivée et variations, position relative.
Exercice N°281 :
Soit la fonction f définie sur R par
f(x)= x2ex − 1 − (x2/2).
Conjectures à partir d’un graphique :
Le graphique ci-dessous est la courbe représentative C de f telle que l’affiche une calculatrice dans un repère orthogonal.
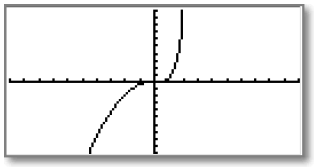
1-2) Grâce à l’observation de cette courbe, conjecturer :
1) – le sens de variation de f, Lis la suite »
Maths de terminale : fonction, exercice, limite, exponentielle, courbe. Variations, dérivée, coordonnées, tangente, continuité, encadrement.
Exercice N°274 :
Exercice N°274 :
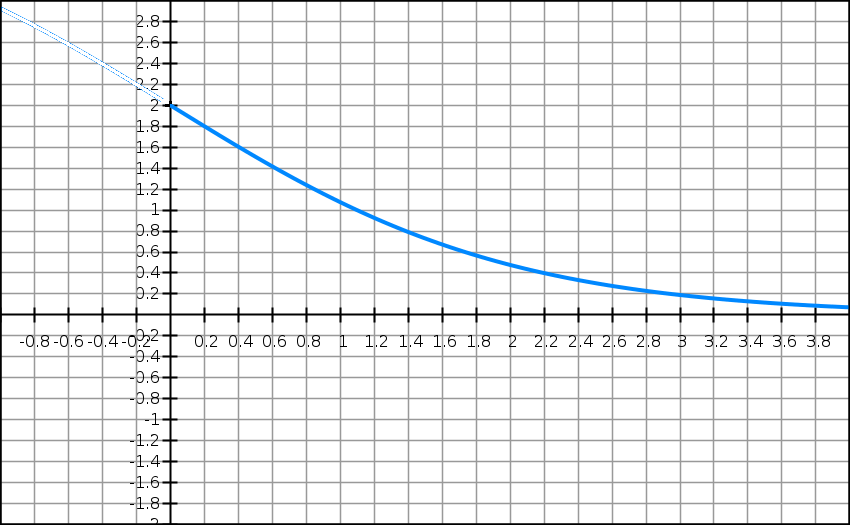
Soit g la fonction définie sur [0 ; +∞[
par g(x) = ex − xex + 1.
(La courbe du dessus n’est pas celle de g.)
1) Déterminer la limite de g en +∞. Lis la suite »
Maths de terminale : exercice d’exponentielle, équation, démonstration, limite, dérivée, variation, croissance comparée, polynôme.
Exercice N°659 :
Exercice N°659 :
Équation à résoudre :
Soit P le polynôme défini par
P(x) = x3 + 2x2 − x − 2.
1) Montrer que P(x) = (x − 1)(x2 + 3x + 2), pour tout réel x. Lis la suite »
Exercice de maths de terminale sur le logarithme népérien, limite, fonction, suite, équation, inéquation, variation, récurrence, convergence.
Exercice N°361 :
Exercice N°361 :
1) ln(32) − ln(3) = ? Lis la suite »
