Maths de terminale : exercice d’exponentielle avec fonction auxiliaire. Continuité, étude de signe, dérivée et variations, position relative.
Exercice N°281 :

Soit la fonction f définie sur R par
f(x)= x2ex − 1 − (x2/2).
Conjectures à partir d’un graphique :
Le graphique ci-dessous est la courbe représentative C de f telle que l’affiche une calculatrice dans un repère orthogonal.
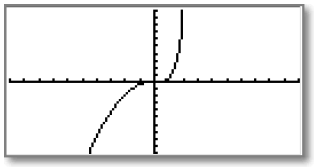
1-2) Grâce à l’observation de cette courbe, conjecturer :
1) – le sens de variation de f,
2) – la position de G par rapport à l’axe des abscisses.
Étude d’une fonction auxiliaire g :
Soit g la fonction définie sur R par
g(x) = (x + 2)ex − 1 − 1.
3) Étudier les limites de g en +∞ et en −∞ (en justifiant soigneusement).
4) Montrer que g ‘ (x) = (x + 3)ex−1 puis faire l’étude de son signe.
5) Dresser le tableau de variation de g. Faire apparaître les limites obtenues.
6) Montrer que l’équation g(x) = 0 admet une solution unique dans R. On notera α cette solution. Montrer que 0,20 < α < 0,21.
7) Déduire des questions précédentes le signe de g(x) suivant les valeurs de x.
Étude de la fonction f :
8) Calculer f ‘ (x) pour tout réel x, et montrer que f ‘ (x) = xg(x).
9) En déduire le signe de f ‘ (x) et dresser le tableau de variation de la fonction f.
Que pensez-vous de votre conjecture faite dans la première question ?
10) Sachant que g(α) = 0, démontrer que
f(α)= −α3/2(α+2).
11) Déterminer le nombre de solutions de l’équation f(x) = 0 et donner une valeur approchée ou exacte de la ou les solutions.
Que pensez-vous de votre deuxième conjecture sur la position de C par rapport à l’axe des abscisses ?
12) Proposer un réglage judicieux de la fenêtre graphique de la calculatrice qui permettra de visualiser les résultats précédents.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, exponentielle, fonction auxiliaire.
Exercice précédent : Exponentielle – Fonction, dérivées, limite, continuité – Terminale

