frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Rédaction :

Les issues possible sont 1, 2, 3 et 4. Donc l’univers est
U = {1 ; 2 ; 3 ; 4}.

2) Explication :

Une loi de probabilité est bien souvent un tableau avec les valeurs concernées sur la première lignes (les x_i) et les probabilités associées sur la seconde ligne
: les p_i = P(X = x_i).

Rédaction :

Il y a autant de chance de piocher chaque jeton car ils sont indiscernables au toucher.
On est donc dans une situation d’équiprobabilité.
La formule de la probabilité d’une issue (résultat) est donc :

Par exemple, pour la valeur 3, il y a 3 jetons donc le nombre de cas favorables est 3 et le nombre total de cas est 1+2+3+4 = 10.

Du coup, P(X = 3) = ³/₁₀ = 0,3.
De même, P(X = 1) = ¹/₁₀ = 0,1 car il y a un seul jeton marqué 1.
P(X = 2) = 0,2.
P(X = 4) = 0,4.

La loi de probabilité est :

3) Rédaction :

Le jeton porte un numéro pair s’il a le numéro 2 ou le numéro 4, donc j’additionne les probabilités du tableau.
P(A) = P(X = 2) + P(X = 4) = 0,2 + 0,4 = 0,6.

4) Rédaction :

Le jeton porte un numéro supérieur ou égal à trois, s’il a le numéro 3 ou 4, donc j’additionne les probabilités du tableau.
P(B) = P(X = 3) + P(X = 4) = 0,3 + 0,4.

5) Rédaction :

A inter B, c’est avoir A « et à la fois » B. Le jeton doit être pair et à la fois supérieur ou égal à 3. Seul 4 fonctionne.
P(A inter B) = P(X = 4) = 0,4.

6) Rédaction :

Comme on a A, B, et A inter B, je peux utiliser la formule de l’union A U B qui est :

P(A U B) = 0,6 + 0,7 – 0,4 = 0,9.

Autre méthode :

Cela revient à vouloir « soit » A (les pairs 2 et 4), « soit » B (3 et 4), « soit » les deux cas en même temps (le pair 4).
Du coup, on accepte 2, 3 et 4 et on additionne les probabilités
0,2 + 0,3 + 0,4 = 0,9. Ce qui revient au même.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) La forme développée est
f(x) = 5x² + 4x – 1
avec a = 5, b = 4, c = -1.

Je calcule Δ = b² – 4ac
= 16 – 4×5×(-1)
= 36 > 0.
Donc le trinôme admet deux racines distinctes :

x₁ = ^{(-b – √Δ)}/_2a
= ^{(-4 – √36)}/₁₀
= ^{(-4 – 6)}/₁₀
= -1

x₂ = ^{(-4 + 6)}/₁₀
= 1/5.

La forme factorisée est
f(x) = a×(x – x₁)×(x – x₂)
= 5(x – (-1))(x – 1/5)
= 5(x + 1)(x – 1/5)

2) La forme canonique d’une fonction polynôme s’écrit :
a(x – x_Sommet)² + y_Sommet
= a(x – α)² + β.

α = x_Sommet = ^-b/_2a
= ^-4/₁₀
= ^-2/₅

β = y_Sommet = ^-Δ/_4a
= ^-36/₂₀
= ^-9/₅

On peut calculer β en faisant f(α) aussi.

Donc f(x) = 5(x – (^-2/₅))² + (^-9/₅)
= 5(x + (²/₅))² – (⁹/₅).

3) Pour étudier le signe, on reprend les racines -1 et 1/5 et on fait le tableau de signe. Le signe de a = 5 est positif. On met le « + » à l’extérieur des racines.

x|-∞ -1 1/5 +∞
signe| + 0 – 0 +

4) Comme a > 0, la parabole est tournée vers le haut.
Comme l’abscisse du sommer est α = ^-2/₅, la fonction est donc
décroissante sur ]-∞ ; ^-2/₅] et
croissante sur [^-2/₅ ; +∞[.

5) Avoir l’intersection d’une courbe avec l’axe des ordonnées, cela veut dire que x = 0 et y = f(0).
On fait donc y = f(0) = 5×0² + 4×0 – 1 = -1.
L’intersection est le point de coordonnées (0 ; -1).

6) Pour avoir les intersections de Cf et de la droite d’équation
y = 4x + 4,
on résout l’équation :
f(x) = 4x + 4

soit 5x² + 4x – 1 = 4x + 4

On soustrait par 4x + 4 pour laisser 0 à droite :
soit 5x² – 5 = 0

On peut calculer le discriminant ou factoriser par 5 :
soit 5(x² – 1) = 0

On factorise (a² – b²) en (a + b)(a – b) :
soit 5(x + 1)(x – 1) = 0

Un produit de facteurs est nul si au moins l’un des facteurs est nul :
soit 5 = 0 ou x + 1 = 0 ou x – 1 = 0

5 est toujours différent de 0 :
soit x = -1 ou x = 1

Les points d’intersection sont (-1 ; f(-1)) et (1 ; f(1))
soit (-1 ; 0) et (1 ; 8).

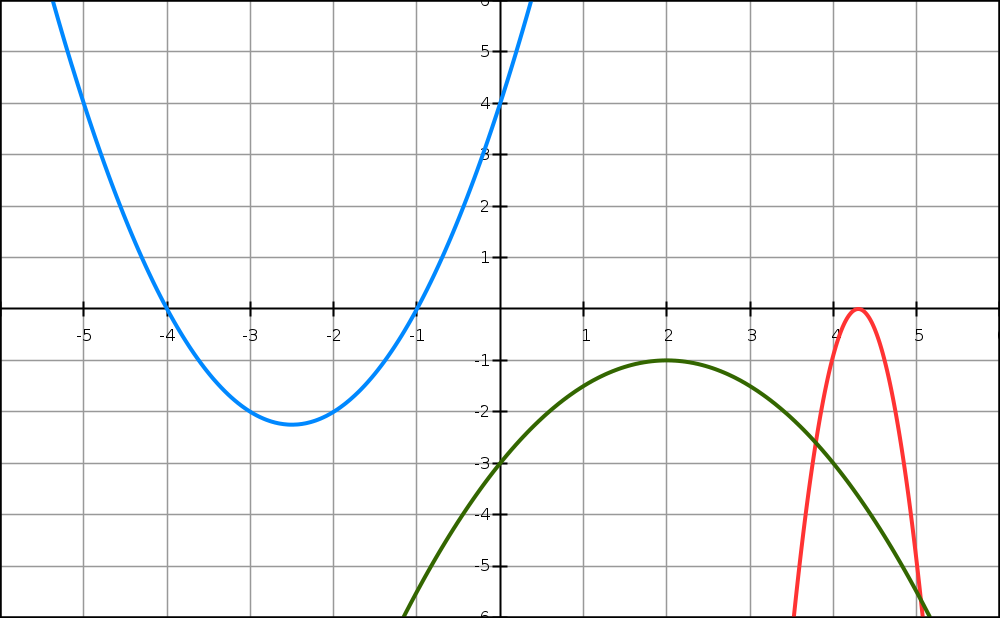
7) (P) a pour sommet S(-1 ; 2) et passe par le point A(2 ; 20).
On a donc les coefficients a, b, c d’un trinôme
g(x) = ax² + bx + c à trouver.

Le sommet a comme abscisse -1 qui vaut ^-b/_2a, cela donne b = 2a.

De plus, g(-1) = 2 et g(2) = 20.
Donc a×(-1)² + b×(-1) + c = a – b + c = 2.
Donc a×2² + b×2 + c = 4a + 2b + c = 20.

On sait que b = 2a donc :
a – 2a + c = 2
4a + 2*2a + c = 20

On obtient le système :
{ -a + c = 2
{ 8a + c = 20

J’isole le c.
{ c = 2 + a
{ c = 20 – 8a

Comme on a c = c, on a 2 + a = 20 – 8a.
9a = 18 donc a = 2.
On remonte à c = 2 + a = 2 + 2 = 4.
Puis à : b = 2×a = 2×2 = 4.
Donc g(x) = 2x² + 4x + 4.

8) (Q) coupe l’axe des abscisses aux points d’abscisses -1 et 5 et l’axe des ordonnées au point d’ordonnée -10.
Cela veut dire que les racines sont -1 et 5.
On peut utiliser la forme factorisée :
h(x) = a(x – x1)(x – x2)
= a(x – (-1))(x – 5)
= a(x + 1)(x – 5)

Sur l’axe des ordonnées, x = 0.
On a h(0) = -10,
soit a(0 + 1)(0 – 5) = -10
soit -5a = -10
soit a = -10/(-5) = 2.

Donc h(x) = 2(x + 1)(x – 5).

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Dans cette situation, il y a deux paramètres à propos des téléphones. Le premier est la présence du Wifi W (ou non) et le second est la présence du GPS G (ou non). Pour représenter cette situation, je te suggère de faire un tableau à double entrées.

Sur les lignes, tu peux séparer W (avec Wifi) et ^–W (sans Wifi). Sur les colonnes, tu peux séparer G (avec GPS) et ^–G (sans GPS).

La ligne du dessous est le sous-total de G et celui de ^–G, la colonne de droite est le sous-total de W et celui de ^–W.

Les quatre cases centrales sont les intersections qui prennent en compte à la fois la présence (ou non) de W et la présence (ou non) de G. Enfin en bas à droite, il y a le total. Ici, on travaille en pourcentage donc on met 100%.

Voici le premier tableau avec ce que l’on cherche en rouge (l’union veut dire qu’on veut au moins G ou W). Les données de l’exercice sont en vert.

Pour compléter les cases, tu dois faire des soustractions sur les lignes et les colonnes.
70 – 24 = 46 ;
40 – 24 = 16 ;
100 – 70 = 30 ;
100 – 40 = 60 ;
30 – 16 ou 60 – 46 = 14
De cette manière, toutes les cases du tableau sont remplies et tu obtiens la répartition des options avec les intersections. Ces résultats sont en bleu foncé ci-dessous.

Pour l’union G U W, on reprend ce qu’il y a en rouge (avec la présence de « soit G, soit W, soit les deux ») et on additionne :
24 + 46 + 16 = 86%.
Donc P(G U W) = 0,86.

2) Aucune des deux options, c’est ni G, ni W, soit « ^–G inter ^–W », c’est la case avec 14%.
P(aucune des deux options)= 0,14.

3) 6 euros correspond à prendre l’option Wifi sans prendre celle du GPS. Dans le tableau, cela revient à prendre « ^–G inter W » qui vaut 46%.
Donc P(X = 6) = 0,46.

4) Une loi de probabilité revient (presque toujours) à faire un tableau avec les valeurs en haut et les probabilités sur la ligne du dessous. Ici, il s’agit de faire la loi de probabilité du gain qui est liée à celle des options (car le gain dépend des options).

On va reprendre le précédent tableau, mais en plus « aplati ».

La première ligne rappelle les options, la deuxième indique le gain, puis la troisième met les probabilités. La loi de probabilité du gain concerne les deux dernières lignes. C’est pour ça que j’ai mis la première ligne entre parenthèses.

5) La formule de l’espérance est :
E(X) = Valeur1 × Proba1 + Valeur2 × Proba2 + Valeur3 × Proba3 + Valeur4 × Proba4
= 0 × 0,14 + 6 × 0,46 + 12 × 0,16 + 18 × 0,24
= 9.

L’espérance est de 9. Cela veut dire qu’en moyenne, la marque va payer 9 euros pour les options.

6) On fait en moyenne 9 × 200000 = 1,8 millions d’euros.

Bonne compréhension,
Sylvain Jeuland