Exercice de maths de terminale avec algorithme, graphique, suite arithmétique, fonction, raisonnement par récurrence, limite.
Exercice N°173 :
On considère la suite (un) définie pour tout n ∈ N par
u0 = -2 et, pour tout entier n,
un+1 = un/(1 – un).
On admet pour commencer que pour tout entier naturel n,
un ≠ 1.
1) Calculer u1 et u2.
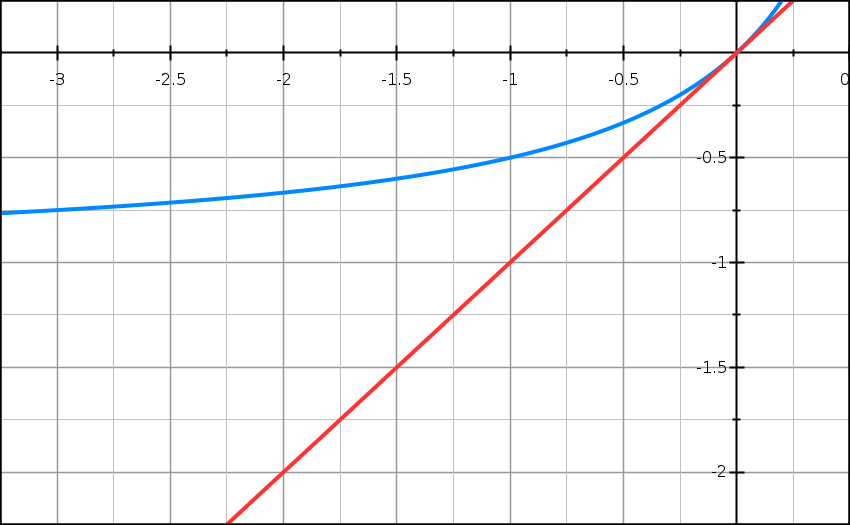
On donne ci-dessus la représentation graphique de la fonction f dans un repère orthonormé du plan. On donne aussi la droite Δ d’équation y = x.
f est définie pour tout x de ]-∞ ; 1[ par
f(x) = x/(1 – x).
2) Construire sur l’axe des abscisses les points A1, A2, A3 d’abscisses respectives u1, u2, u3.
3) Montrer par récurrence que pour tout entier n, on a
un < 0.
4) En déduire que la suite (un) est croissante.
5) Quelle semble être la limite de la suite (un) ?
6) Écrire un algorithme permettant de trouver le plus petit entier N tel que :
Pour tout n ≥ N, |un| < 10-2.
7) Déterminer cette valeur à l’aide de la calculatrice.
On considère la suite numérique (vn) définie pour tout n ∈ N par
vn = (un – 4)/un.
On admettra que pour tout entier naturel n,
vn ≠ 1.
8) Démontrer que (vn) est une suite arithmétique de raison 4.
9) En déduire l’expression de vn en fonction de n.
10) Exprimer un en fonction de vn, puis en déduire que
un = – 2/(2n + 1).
11) Vérifier le résultat trouvé en 7) à l’aide du résultat précédent.
Soit α un réel positif.
12) Déterminer le plus petit entier naturel N tel que :
Pour n ≥ N, |un| < α.
13) En déduire la limite de la suite (un).
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : algorithme, graphique, suite, arithmétique.
Exercice précédent : Suites – Somme, conjecture, raisonnement par récurrence – Terminale

