Maths de terminale : exercice de récurrence avec suite et somme. Calcul des premiers termes, raisonnement, conjecture et formule explicite.
Exercice N°172 :
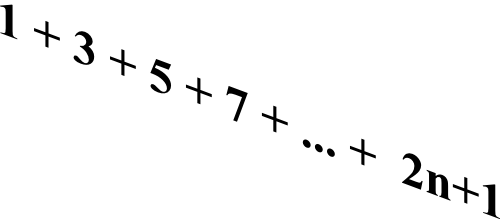
On considère la suite (un) définie pour tout entier naturel n par l’expression :
un = 1 + 3 + … + (2n + 1) = Σnp=0(2p + 1)
1) Établir une relation de récurrence entre les termes un+1 et un.
2) Calculer les termes u0, u1, u2, u3 et u4.
3) A l’aide la question précédente, conjecturer l’expression explicite du terme un, en fonction de n.
4) A l’aide d’un raisonnement par récurrence, démontrer cette conjecture.
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : exercice, récurrence, suite, somme.
Exercice précédent : Probabilités – Variable aléatoire et loi binomiale – Terminale

