Maths de seconde : exercice de fonction avec images, antécédents. Résolution graphique d’inéquations, courbe, domaine de définition.
Exercice N°201 :
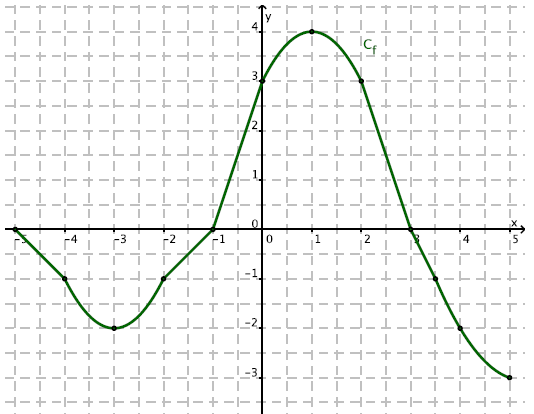
1) Déterminer le domaine de définition D de la fonction f représentée ci-dessus. Lis la suite »
Fonctions – Bases, images, antécédents, inéquations – Seconde
16 septembre 2020
Fonctions – Bases, résolution graphique, courbe – Seconde
16 septembre 2020
Exercice de maths de seconde sur les fonctions. Résolution graphique, fonction bénéfice, courbe, équation, inéquation, antécédent, image.
Exercice N°200 :
L’entreprise Jardi+ fabrique chaque jour une quantité x d’articles de jardinage, avec x ∈ [0 ; 140].
Le coût total de production, en euros, en fonction de x, est donné par la fonction f, dont la représentation graphique Cf se trouve ci-contre.
La demi-droite représente la recette R(x) en fonction du nombre d’outils vendus. Le bénéfice est la différence entre la recette et le coût de production.
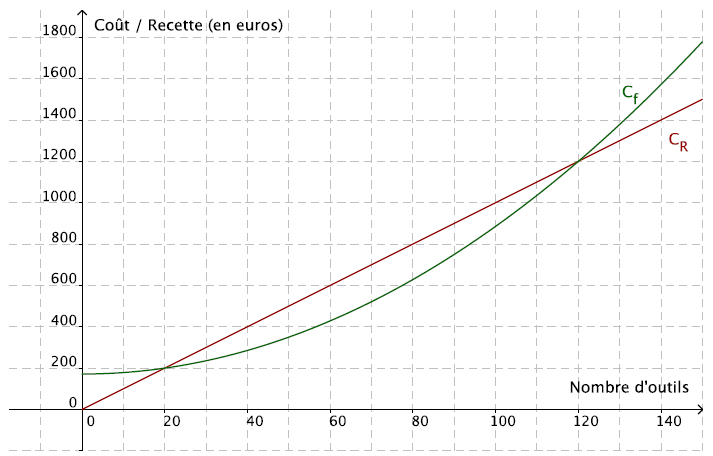
1) Déterminer graphiquement le bénéfice réalisé pour la vente de 100 outils. Lis la suite »
Fonctions – Bases, définition, variations, équations – Seconde
16 septembre 2020
Maths de seconde : exercice de fonction avec équations et graphique. Domaine de définition, points, tableau de variation, résolution.
Exercice N°199 :
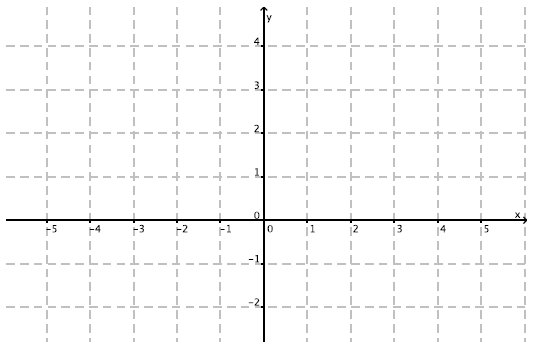
1) Placer les points suivants donnés par leurs coordonnées :
O(0 ; 0), A(-3 ; 3), B(1 ; 1), C(3 ; 1), D(4 ; 2)
dans le repère orthonormé suivant, puis relier ces points par des segments de droites de façon à obtenir la courbe représentative d’une fonction f. Lis la suite »
Fonctions – Lecture graphique, convexité, coût moyen – Terminale
16 septembre 2020
Exercice de maths de terminale sur les fonctions. Exercices, lecture graphique, convexité et point d’inflexion, coût moyen, variation.
Exercice N°406 :
Une entreprise fabrique de l’huile de massage. Le coût total de production de q litres de parfum par jour est donné par une fonction représentée ci-dessous. On a également représenté la tangente à la courbe au point 5.
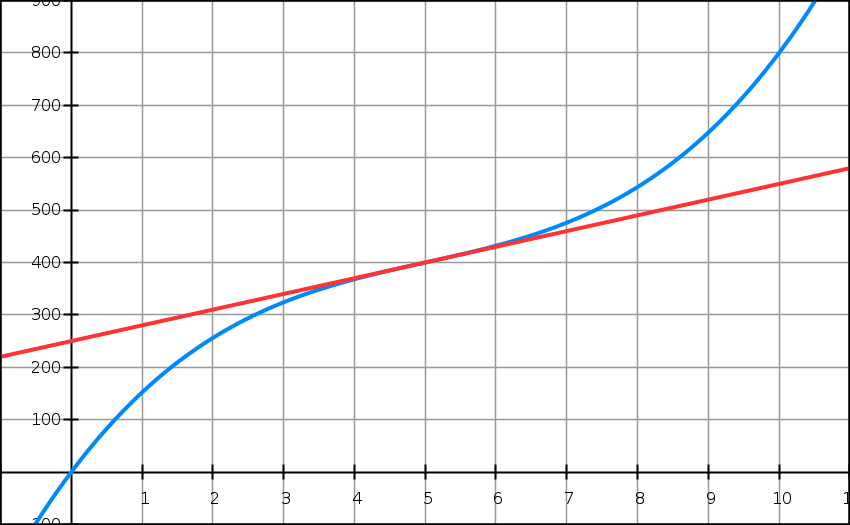
1-2-3-4) En se servant du graphique répondre par Vrai ou Faux et justifier : Lis la suite »
Statistiques – Lancer de dés et aires de triangles – Seconde
16 septembre 2020
Maths de seconde : exercice de statistiques avec ECC et diagramme en bâtons. Moyenne, médiane, quartiles. Tableau d’aire, triangle aléatoire.
Exercice N°011 :
Un jeu consiste à lancer six fois de suite un dé :
- les résultats affichés sont considérés, dans l’ordre de sortie, comme les coordonnées xA, yA, xB, yB, xC, yC, de trois points A, B, C du plan muni d’un repère orthonormé d’unité 1 cm. Par exemple : si les 6 lancers successifs donnent dans l’ordre :
3 ; 5 ; 2 ; 2 ; 6 ; 4
alors les points associés sont A(3 ; 5), B(2 ; 2), C(6 ; 4).
<
- On s’intéresse alors à l’aire du triangle ABC ainsi obtenu. Dans l’exemple précédent, l’aire de ABC serait 5 cm2.
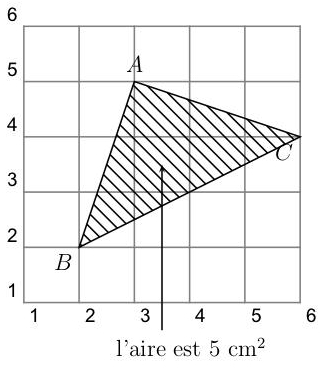
On a joué 100 fois à ce jeu et on a relevé, pour chaque partie jouée, l’aire obtenue (en cm2, tronquée à l’entier inférieur). Tous les résultats sont regroupés dans le tableau ci-dessous :
1) Représenter le diagramme en bâtons des effectifs cumulés croissants de cette série statistique (unité 1 cm pour les aires et 1 mm pour les effectifs). Lis la suite »
Livre de maths de seconde – L’addition de nombres entiers – Page 11
16 septembre 2020
Fonctions – Étude graphique et tableau de variations – Seconde
16 septembre 2020
Maths de seconde : exercice de fonctions avec résolution graphique d’équation et d’inéquation. Tableaux de signe, variation.
Exercice N°010 :
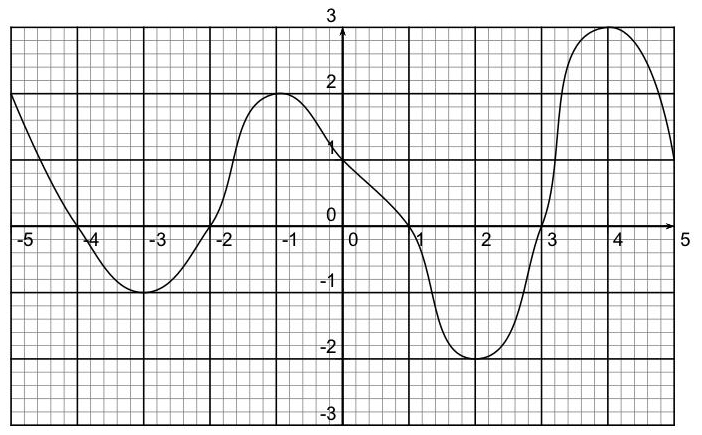
On considère la fonction la fonction f définie [-5 ; 5] et représentée ci-dessus.
1) Lire graphiquement les images de 2 et de 3 par la fonction f. Lis la suite »
Corrigé
15 septembre 2020
Exercice : Clic droit vers l’exercice
Tout le corrigé :
(E1) : cos(x) = 1/2
(E2) : sin(2x + π/6) = √2/2
1) (E1) :
Rédaction :
En traçant le cercle trigonométrique et en dessinant un trait vertical au niveau de x = 1/2 (car le cosinus représente l’abscisse), on s’aperçoit que 1/2 est le cosinus de π/3 et de –π/3.
Donc cos(x) = 1/2
⇔ cos(x) = cos(π/3)
Hors rédaction :
Pour obtenir les valeurs de l’angle x sans les cosinus, on utilise la propriété du cours qui découle du dessin suivant :
Si deux angles ont le même cosinus, ici a et b, alors ces deux angles sont égaux (a = b) ou opposés (l’un vers le haut, l’autre vers le bas : a = -b). Ceci au nombre de tours complets près : on peut ajouter des 2π comme l’indique la flèche rouge qui fait un tour complet.
Rédaction :
Comme :
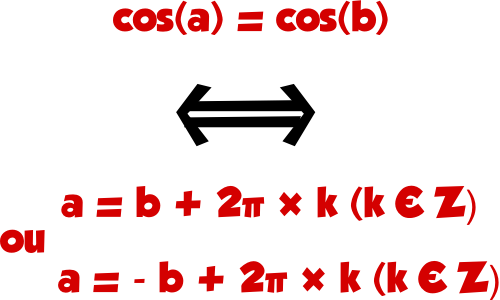
On a donc
cos(x) = cos(π/3)
⇔
x = π/3 + 2π × k (k ∈ Z)
ou
x = –π/3 + 2π × k (k ∈ Z).
L’ensemble des solutions sur R est l’ensemble des angles
{π/3 + 2π × k (k ∈ Z) ;
–π/3 + 2π × k (k ∈ Z)}
(E2) :
En traçant le cercle trigonométrique et en dessinant un trait horizontal au niveau de y = √2/2 (car le sinus représente l’ordonnée), on s’aperçoit que √2/2 est le sinus de π/4 et de 3π/4.
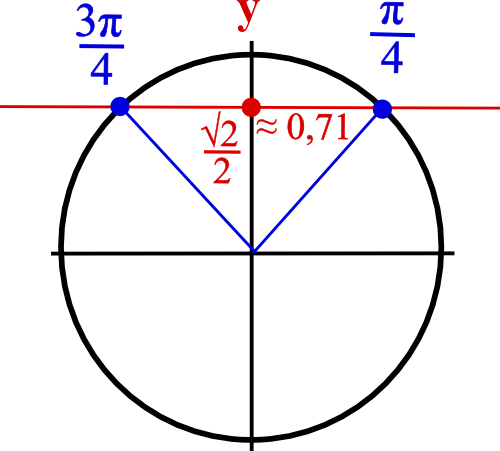
Donc sin(2x + π/6) = √2/2
⇔ sin(2x + π/6) = sin(π/4)
Hors rédaction :
Pour obtenir les valeurs de l’angle x sans les sinus, on utilise la propriété du cours qui découle du dessin suivant :
>
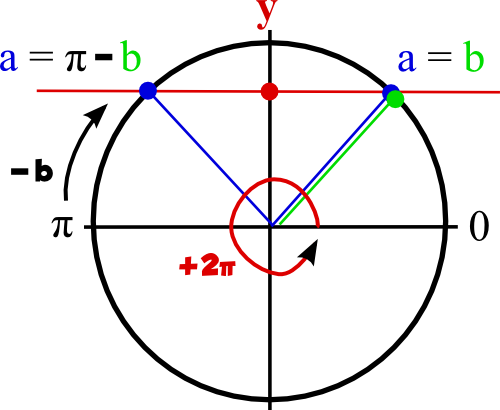
Si deux angles ont le même sinus, ici a et b, alors ces deux angles sont égaux (a = b) ou opposés par rapport à l’axe des ordonnées (l’un vers la droite, l’autre vers la gauche : a = π-b). Ceci au nombre de tours complets près : on peut ajouter des 2π comme l’indique la flèche rouge qui fait un tour complet.
Rédaction :
Comme :
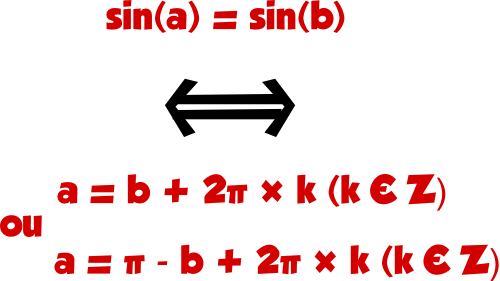
On a donc
sin(2x + π/6) = sin(π/4)
⇔
2x + π/6 = π/4 + 2π × k (k ∈ Z)
ou
2x + π/6 = π – π/4 + 2π × k (k ∈ Z)
⇔
2x = π/4 – π/6 + 2π × k (k ∈ Z)
ou
2x = π – π/4 – π/6 + 2π × k (k ∈ Z)
⇔
2x = π/12 + 2π × k (k ∈ Z)
ou
2x = 7π/12 + 2π × k (k ∈ Z)
⇔
x = π/24 + π × k (k ∈ Z)
ou
x = 7π/24 + π × k (k ∈ Z)
Ici on fait attention à bien diviser les 2π !
L’ensemble des solutions sur R est l’ensemble des angles
{π/24 + π × k (k ∈ Z) ;
7π/24 + π × k (k ∈ Z)}
2) (E1) :
Rédaction :
On reprend les solutions sur R :
{π/3 + 2π × k (k ∈ Z) ;
–π/3 + 2π × k (k ∈ Z)}
Ici je vois que le dénominateur est 3, donc je mets l’intervalle demandé sur 3 aussi.
]-π ; π] = ]-3π/3 ; 3π/3]
Si on enlève le π du haut, l’intervalle entier à considérer sera ]-3 ; 3].
π/3 + 2π × k (k ∈ Z) :
Je teste les « k » vers les négatifs en partant de 0.
k = 0 :
π/3 + 2π × 0
= π/3
Dans l’intervalle, OK.
k = -1 :
π/3 + 2π × (-1)
= π/3 – 6π/3
= –5π/3
-5 est en dessous de -3, donc on n’est plus dans l’intervalle solutions, du coup on ne prend pas cette valeur.
On est trop bas, maintenant je passe au k positifs.
k = 1 :
π/3 + 2π × 1
= π/3 + 6π/3
= 7π/3
7 est au dessus de 3, donc on n’est plus dans l’intervalle solutions, du coup on ne prend pas cette valeur. On s’arrête.
–π/3 + 2π × k (k ∈ Z)
Je teste les « k » vers les négatifs en partant de 0.
k = 0 :
–π/3 + 2π × 0
= –π/3
Dans l’intervalle, OK.
k = -1 :
–π/3 + 2π × (-1)
= –π/3 – 6π/3
= –7π/3
-7 est en dessous de -3, donc on n’est plus dans l’intervalle solutions, du coup on ne prend pas cette valeur.
On est trop bas, maintenant je passe au k positifs.
k = 1 :
–π/3 + 2π × 1
= –π/3 + 6π/3
= 5π/3
5 est au dessus de 3, donc on n’est plus dans l’intervalle solutions, du coup on ne prend pas cette valeur. On s’arrête.
Du coup, S = {π/3 ; –π/3}
(E2) :
Rédaction :
On reprend les solutions sur R :
{π/24 + π × k (k ∈ Z) ;
7π/24 + π × k (k ∈ Z)}
Ici je vois que le dénominateur est 24, donc je mets l’intervalle demandé sur 3 aussi.
]-π ; π] = ]-24π/24 ; 24π/24]
Si on enlève le π du haut, l’intervalle entier à considérer sera ]-24 ; 24].
π/24 + π × k (k ∈ Z) :
Je teste les « k » vers les négatifs en partant de 0.
k = 0 :
π/24 + π × 0
= π/24.
Dans l’intervalle, OK.
k = -1 :
π/24 + π × (-1)
= –23π/24.
-23 est dans l’intervalle ]-24 ; 24].
Donc OK.
k = -2 :
π/24 + π × (-2)
= –47π/24.
Non, on n’y est plus.
k = 1 :
π/24 + π × 1
= 25π/24.
25 est au dessus de 24, on n’y est plus.
On s’arrête.
7π/24 + π × k (k ∈ Z) :
Je teste les « k » vers les négatifs en partant de 0.
k = 0 :
7π/24 + π × 0
= 7π/24.
7 entre -24 exclu et 24 inclus. OK.
k = -1 :
7π/24 + π × (-1)
= -17π/24.
-17 entre -24 exclu et 24 inclus. OK.
k = -2 :
7π/24 + π × (-2)
= -41π/24.
Trop bas.
k = 1 :
7π/24 + π × 1
= 31π/24.
31 > 24, trop haut. On s’arrête là.
Du coup, S = {π/24 ; –23π/24 ; 7π/24 ; -17π/24}.
f : x → sin(x)/(2 – cos(x))
3) Rédaction :
2-cos(x) est toujours différent de 0 car cos est toujours entre -1 et 1.
Du coup, le dénominateur est toujours différent de zéro, donc f est dérivable quand le numérateur sin(x) est dérivable (R) et le dénominateur (2-cos(x)) est dérivable (R).
Par conséquent, f est dérivable sur R.
4) Rédaction :
Pour montrer qu’une fonction est impaire, il faut démontrer que :
pour tout x, f(-x) = -f(x).
Pour tout x, f(-x) = sin(-x)/(2 – cos(-x))
= -sin(x)/(2 – cos(x))
(car sin étant impaire, sin(-x) = -sin(x). Et cos étant paire, cos(-x) = cos(x))
= –sin(x)/(2 – cos(x))
= -f(x).
Donc f est impaire et la courbe Cf est donc symétrique par rapport à l’origine du repère.
5) Rédaction :
Pour montrer qu’une fonction est périodique de période 2π, je dois montrer que :
pour tout x, f(x + 2π) = f(x).
Pour tout x, f(x + 2π)
= sin(x + 2π)/(2 – cos(x + 2π))
= sin(x)/(2 – cos(x))
(sin et cos sont périodique de période 2π donc sin(x + 2π) = sin(x) et
cos(x + 2π) = cos(x))
= f(x).
Donc f est 2π-périodique.
6) Rédaction :
Si on a f sur [0 ; π], on aura f sur [-π ; 0] car comme f est impaire, il suffit de prendre l’opposé des valeurs de f(x).
On a donc f sur [-π ; π]. Comme f est 2π-périodique, il suffit de reprendre les valeurs sur cet intervalle pour avoir les valeurs sur [π ; 3π], et ainsi de suite par translation de 2π.
7) Rédaction :
f(x) = u(x)/v(x)
avec u(x) = sin(x)
u'(x) = cos(x)
v(x) = 2 – cos(x)
v'(x) = -(-sin(x)) = sin(x)
f'(x) = (u'(x)v(x) – u(x)v'(x))/(v(x)2)
= (cos(x)(2 – cos(x)) – sin(x)sin(x))/(2 – cos(x)2)
= (2cos(x) – cos(x)2 – sin(x)2)/(2 – cos(x)2)
= (2cos(x) – [cos(x)2 + sin(x)2])/(2 – cos(x)2)
= (2cos(x) – 1)/(2 – cos(x)2).
8) Rédaction :
Numérateur : 2cos(x) – 1 ≥ 0
quand 2cos(x) ≥ 1
quand cos(x) ≥ 1/2
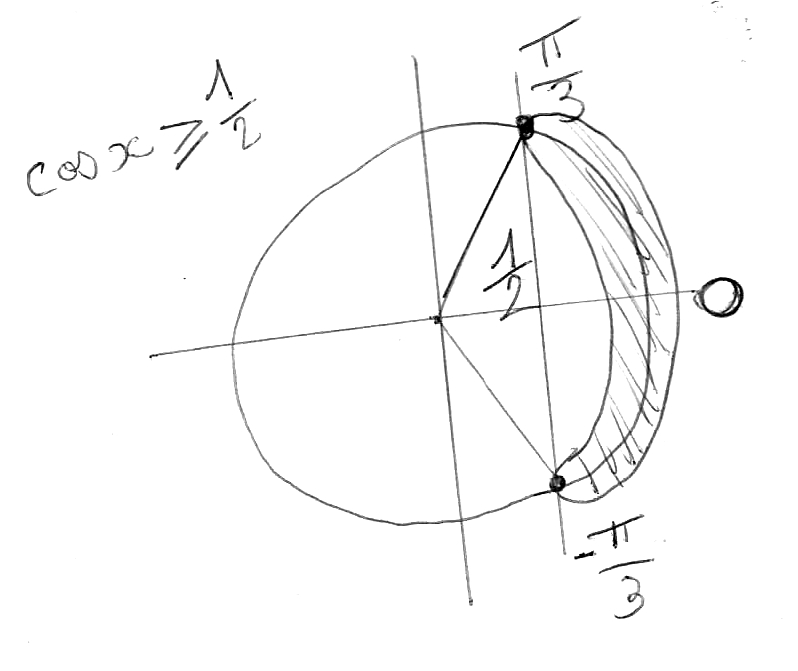
Le cosinus est supérieur à 1/2 quand x est entre –π/3 et π/3. Donc entre 0 et π/3 sur notre intervalle.
Dénominateur : Il n’est jamais égal à zéro et c’est un carré. Donc toujours +.
Voici le tableau de signe de f'(x).
9) Voir ci-dessus.
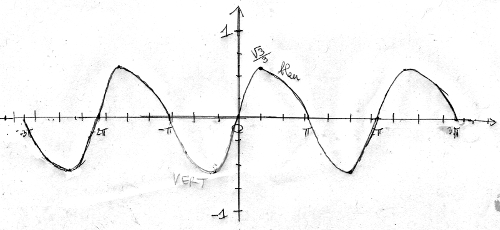
10) 
Bonne compréhension,
Sylvain Jeuland
Second degré – Géométrie 2D, graphique, droite, fonction – Première
14 septembre 2020
Maths de première : exercice de second degré, géométrie, vecteur, les droites et tangente, résolution d’équation, interprétation graphique.
Exercice N°384 :
Exercice N°384 :
Dans un repère orthonormé du plan, d est la droite
passant par le point A(1 ; −3)
et dirigée par le vecteur →u(1 ; 2).
f est une fonction définie sur R par
f(x) = 3x2 −2x − 4
et représentée par Cf dans le repère.
1) Faire une figure soignée représentant la fonction et la droite. Lis la suite »
Second degré et Géométrie 2D – Carré, triangle, aires – Première
14 septembre 2020
Maths de première : exercice de second degré et les aires. Carré, rectangle, géométrie, polynôme, maximum, signe, inéquation, surfaces.
Exercice N°544 :
ABCD est un carré de 10 cm de côté et AMPN un carré de côté x tel que x appartient à l’intervalle
I = [0 ; 10].
On désigne par S(x) l’aire, en cm2, de la partie grise.
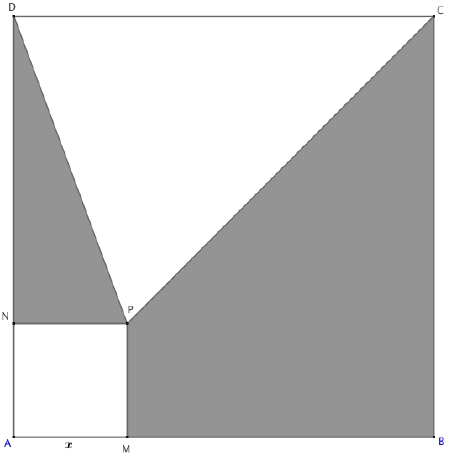
1) Exprimer l’aire du carré AMPN puis celle du triangle CDP en fonction de x. Lis la suite »
