frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers le corrigé

Tout le corrigé :

1) Montrer que C, I et J sont alignés :

Rédaction :

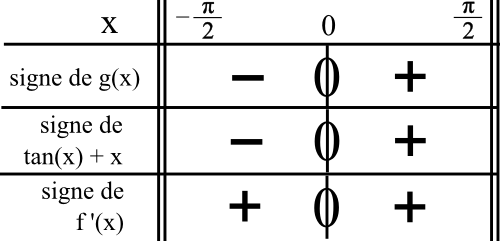
C, I et J sont alignés, si et seulement si, les vecteurs ^→CI et ^→IJ sont colinéaires. J’ai donc besoin des coordonnées de ces vecteurs, donc je dois calculer les coordonnées de C, I et J avant.

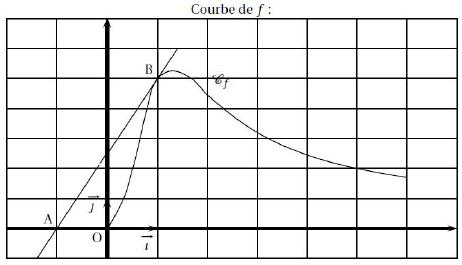
Cette figure est composé de trois carrés dont celui de gauche ABGH. Comme ^→AB et ^→AH ne sont pas colinéaires (côtés du carré), on peut introduire le repère (A ; ^→AB ; ^→AH).

Cela veut dire que le point A a pour coordonnées (0 ; 0), B(1 ; 0) et H(0 ; 1).
Du coup, on a C(2 ; 0), D(3 ; 0), E(3 ; 1), F(2 ; 1) et G(1 ; 1).

Calculons les coordonnées du point I :

I est le milieu de [AG].
Les coordonnées d’un milieu pour deux points A et B sont :

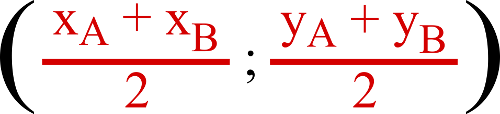
Du coup, je calcule ceci pour [AG].

x_I = ^{(x_A + x_G)}/₂
= ^{(0 + 1)}/₂
= ¹/₂

y_I = ^{(y_A + y_G)}/₂
= ^{(0 + 1)}/₂
= ¹/₂

Du coup, les coordonnées de I sont (¹/₂ ; ¹/₂).

Calculons les coordonnées du point J :

L’abscisse de J est 1 car J est sur [BG] et [BG] relie deux points d’abscisses 1.
L’ordonnée de J est la distance qui le sépare de B, c’est à dire BJ, car l’ordonnée de B est de 0 et car (BJ) est parallèle à la droite (AH) avec ^→AH le vecteur « ordonnées » du repère.

Pour calculer (BJ), on utilise le théorème de Thalès dans le triangle ADE avec :
* (DE) // (BJ),
* (BD) et (JE) sécantes en A,
* A,B,D puis A,J,E alignés dans le même sens.

Du coup, le rapport BJ/DE est égale à AB/AD qui est de ¹/₃ car [AD] c’est trois fois le côté [AB]. Comme DE = 1, on a BJ = ¹/₃, qui donne l’oordonnée du point J ¹/₃.

Du coup, J(1 ; ¹/₂).

Calcul des coordonnées des vecteurs ^→CI et ^→IJ :

x_^→CI
= x_I – x_C
= ¹/₂ – 2
= –³/₂

y_^→CI
= y_I – y_C
= ¹/₂ – 0
= ¹/₂

x_^→IJ
= x_J – x_I
= 1 – ¹/₂
= ¹/₂

y_^→IJ
= y_J – y_I
= ¹/₃ – ¹/₂
= ²/₆ – ³/₆
= –¹/₆

Les deux vecteurs sont colinéaires si et seulement si leurs coordonnées x et x’, puis y et y’ sont proportionnelles.

On a donc le tableau :
–³/₂ | ¹/₂
¹/₂ | –¹/₆

Les produits en croix sont :
–³/₂ × –¹/₆
= +³/₁₂
= ¹/₄
Et :
¹/₂ × ¹/₂
= ¹/₄

Donc les produits en croix sont égaux, x’y – xy’ = 0, les coordonnées sont proportionnelles, donc les vecteurs ^→CI et ^→IJ sont colinéaires et les points C, I et J sont alignés.

2) Montrer que Dm est une droite :

Rédaction :

Quelque soit le m, l’équation mx + (2m – 1)y + 4 = 0
est de la forme ax + by + c = 0 qui est l’équation cartésienne d’une droite.

Du coup, les Dm sont des droites.

3) Trouver m tels que Dm parallèle aux axes :

Rédaction :

D_m est parallèle à l’axe des abscisses si l’équation
est de la forme y = constante.
Ce qui équivaut à y – constante = 0 en mode « équation cartésienne ».
Pour cela, il faut que le coefficient devant x, le « a » soit égal à zéro.
Ce coefficient est « m ». Du coup D_{1 est parallèle à l’axe des abscisses pour m = 0.}

D₁ est parallèle à l’axe des ordonnées si l’équation
est de la forme x = constante.
Ce qui équivaut à x – constante = 0 en mode « équation cartésienne ».

Pour cela, il faut que le coefficient devant y, le « b » soit égal à zéro.
Ce coefficient est (2m – 1). Du coup D_m est parallèle à l’axe des abscisses pour 2m – 1 = 0 soit m = ¹/₂.

4) Équation des droites D₀ et D₁ et point d’intersection :

Rédaction :

L’équation est mx + (2m – 1)y + 4 = 0.

D₀ : 0x + (2 × 0 – 1)y + 4 = 0
⇔ – 1y + 4 = 0
⇔ y = 4.

D₁ : 1x + (2 × 1 – 1)y + 4 = 0
⇔ x + 1y + 4 = 0.

Le point d’intersection, que j’appelle I, est à la fois sur D₀ et D₁ donc les coordonnées de I respectent à la fois les deux équations, donc le système suivant :

{ y = 4
{ x + y + 4 = 0
(Les deux petites accolades sont en fait une seule grande accolade)

⇔
{ y = 4
{ x + 4 + 4 = 0

⇔
{ y = 4
{ x + 8 = 0

⇔
{ y = 4
{ x = -8

Les coordonnées du point d’intersection I sont (4 ; -8).

5) Montrer que que Dm passe par un point fixe :

Rédaction :

Si toutes les droites Dm passent par un point fixe, c’est le point fixe qu’on vient de trouver juste au dessus. C’est à dire I(4 ; -8).

Je dois donc prouver que ce point I appartient à toutes les droites Dm. Donc que ses coordonnées vérifient l’équation-égalité Dm quel que soit le m.

Du coup, quel que soit m,
Gauche = mx + (2m – 1)y + 4
= m × (-8) + (2m – 1) × 4 + 4
= -8m + 8m – 4 + 4
= 0m + 0
= 0 = Droite.

Donc l’équation des droites Dm est vérifiée par ce point. Donc toutes les droites appartiennent à un point fixe quel que soit m.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Rédaction :

Pour montrer qu’une fonction est impaire, il faut montrer que l’image de -x par la fonction g vaut l’opposé de l’image de x. Soit g(-x) = -g(x).

Donc pour tout x,
g(-x) = tan(-x) – (-x)
= -tan(x) + x (car la fonction tan est impaire : sin/cos donc impaire/paire qui est impaire car -/+ donne -)
= -(tan(x) – x)
= -g(x).
Donc g est impaire.

2) Rédaction :

En –^Π/₂ supérieur :

lim_{[x → –^Π/2 sup]} tan(x) = -∞.
lim_{[x → –^Π/2 sup]} x = –^Π/₂ sup.

Par somme/différence, lim_{[x → –^Π/2 sup]} g(x) = -∞.

De la même manière, lim_{[x → +^Π/2 inf]} g(x) = +∞ (car tan tend vers +∞).

3) Rédaction :

Pour étudier les variations de g, calculons sa dérivée.
Pour tout x,
g(x) = tan(x) – x
donc pour tout x,
g'(x) = tan'(x) – 1

Donc g'(x) = (tan(x))² + 1 – 1 = (tan(x))².

Comme un carré est toujours positif ou nul, (tan(x))² est toujours positif. Il sera nul seulement en 0 car seul tan(0) = 0.

Le tableau est donc :

4) Rédaction :

g(0) = tan(0) – 0 = 0 – 0 = 0.
Je mets la valeur 0 dans le tableau ci-dessus.

5) Rédaction :

Pour tout x,
f(x) = tan(x) – x – ^x3/₃

pour tout x,
f'(x) = tan'(x) – 1 – 3^x2₃

Donc f'(x) = (tan(x))² + 1 – 1 – ^{x2
= (tan(x))2 – x2.}

6) Rédaction :

f'(x) = (tan(x))² – x²
= a² – b² (troisième identité remarquable)
= (a – b)(a + b)
= [tan(x) – x] × [tan(x) + x]
= g(x) × [tan(x) + x]

x et tan(x) sont négatifs avant 0 et positifs après 0, donc leur somme également.
Le tableau de signe est :

7) Rédaction :

Comme f'(x) est positif sur Df, f est croissante sur Df.

8) Signe de f(x) et inégalité :

Rédaction

On a la variation de f et,
f(0) = tan 0 – 0 – 0 = 0 – 0 – 0 = 0.
Donc le tableau est :

On a donc f(x) ≤ 0 sur ] –^Π/₂ ; 0 ]
et f(x) ≥ 0 sur [ 0 ; ^Π/₂ [.

Donc tan x – x – ^x3/₃ ≤ 0 sur ] –^Π/₂ ; 0 ].
Et tan x – x – ^x3/₃ ≥ 0 sur [ 0 ; ^Π/₂ [.

Du coup, tan x ≤ x + ^x3/₃ sur ] –^Π/₂ ; 0 ].
Et tan x ≥ x + ^x3/₃ sur [ 0 ; ^Π/₂ [.

Donc ce n’est pas vrai pour les x positifs.

Bonne compréhension,
Sylvain Jeuland