Exercice de maths de terminale de fonction avec courbe, équation réduite, point d’inflexion, tangente, graphique, variation, bénéfice.
Exercice N°404 :
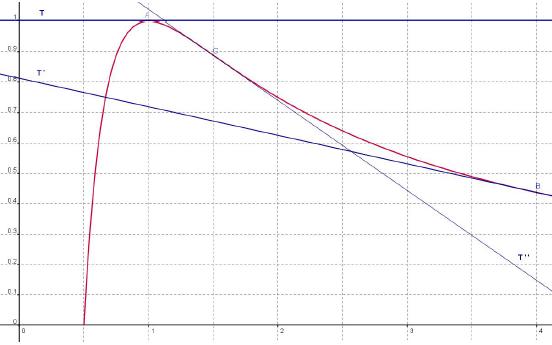
On donne ci-dessus la représentation graphique de la fonction f définie sur [0,5 ; 10] et on note Cf la représentation graphique de la fonction f.
T, T ‘ et T ‘ ‘ sont les tangentes à la courbe au points A d’abscisse 1 et B d’abscisse 4 et C d’abscisse 3/2.
Partie A – En utilisant le graphique :
1) Déterminer f ‘ (1) et donner une valeur approchée aux dixièmes de f ‘ (4).
2) Donner l’équation réduite de la tangente T à Cf au point A.
3) Par lecture graphique, donner l’intervalle pour lequel f est convexe.
Partie B :
f(x) = (2x – 1)/x2.
4) Montrer que
f ‘ (x) = (-2x + 2)/x3
et que
f ‘ ‘(x) = (4x – 6)/x4.
5) Dresser le tableau de variation de f.
6) Dresser le tableau de variation de f ‘ et en déduire la convexité de f.
7) Cf admet-elle un point d’inflexion ?
Si oui, préciser son abscisse et contrôler la cohérence du résultat avec la partie A.
Partie C :
f modélise les bénéfices d’une entreprise en dizaines de milliers d’euros à partir du sixième mois de l’année 2010.
L’axe des abscisses représente le nombre d’années écoulées.
8) Déterminer à quel moment le bénéfice est maximum et son montant en euros.
A partir de x = 1, les bénéfices ont commencé à diminuer mais la baisse des bénéfices s’est ralentie au fil des mois.
9) Déterminer à partir de quelle date a eu lieu le ralentissement de la baisse de ces bénéfices.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : point, inflexion, tangente, graphique.
Exercice précédent : Fonctions – Polynôme, bénéfice, variation, rationnelle – Terminale

