frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Rédaction :

Pour montrer qu’une fonction est impaire, il faut montrer que l’image de -x par la fonction g vaut l’opposé de l’image de x. Soit g(-x) = -g(x).

Donc pour tout x,
g(-x) = tan(-x) – (-x)
= -tan(x) + x (car la fonction tan est impaire : sin/cos donc impaire/paire qui est impaire car -/+ donne -)
= -(tan(x) – x)
= -g(x).
Donc g est impaire.

2) Rédaction :

En –^Π/₂ supérieur :

lim_{[x → –^Π/2 sup]} tan(x) = -∞.
lim_{[x → –^Π/2 sup]} x = –^Π/₂ sup.

Par somme/différence, lim_{[x → –^Π/2 sup]} g(x) = -∞.

De la même manière, lim_{[x → +^Π/2 inf]} g(x) = +∞ (car tan tend vers +∞).

3) Rédaction :

Pour étudier les variations de g, calculons sa dérivée.
Pour tout x,
g(x) = tan(x) – x
donc pour tout x,
g'(x) = tan'(x) – 1

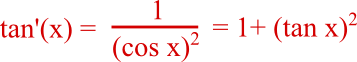
Donc g'(x) = (tan(x))² + 1 – 1 = (tan(x))².

Comme un carré est toujours positif ou nul, (tan(x))² est toujours positif. Il sera nul seulement en 0 car seul tan(0) = 0.

Le tableau est donc :

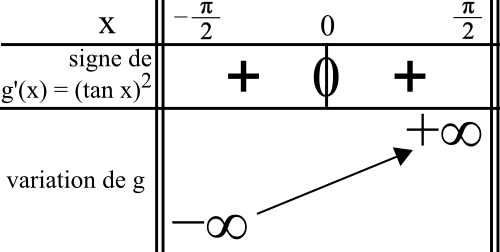
4) Rédaction :

g(0) = tan(0) – 0 = 0 – 0 = 0.
Je mets la valeur 0 dans le tableau ci-dessus.

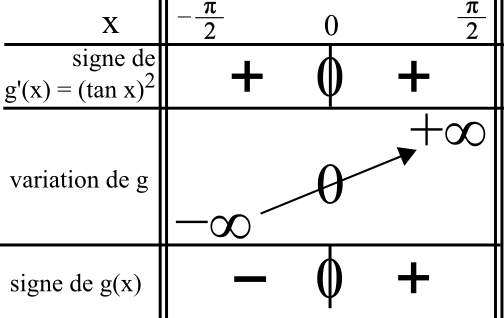
5) Rédaction :

Pour tout x,
f(x) = tan(x) – x – ^x3/₃

pour tout x,
f'(x) = tan'(x) – 1 – 3^x2₃

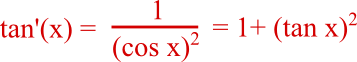
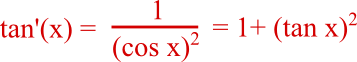
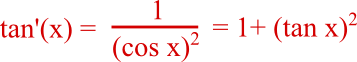
Donc f'(x) = (tan(x))² + 1 – 1 – ^{x2
= (tan(x))2 – x2.}

6) Rédaction :

f'(x) = (tan(x))² – x²
= a² – b² (troisième identité remarquable)
= (a – b)(a + b)
= [tan(x) – x] × [tan(x) + x]
= g(x) × [tan(x) + x]

x et tan(x) sont négatifs avant 0 et positifs après 0, donc leur somme également.
Le tableau de signe est :

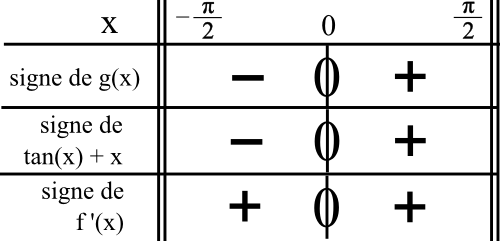
7) Rédaction :

Comme f'(x) est positif sur Df, f est croissante sur Df.

8) Signe de f(x) et inégalité :

Rédaction

On a la variation de f et,
f(0) = tan 0 – 0 – 0 = 0 – 0 – 0 = 0.
Donc le tableau est :

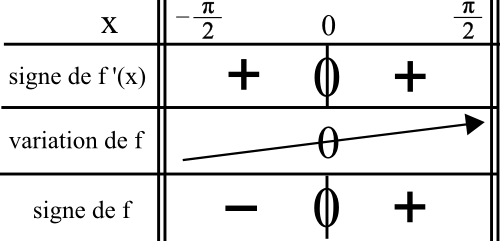
On a donc f(x) ≤ 0 sur ] –^Π/₂ ; 0 ]
et f(x) ≥ 0 sur [ 0 ; ^Π/₂ [.

Donc tan x – x – ^x3/₃ ≤ 0 sur ] –^Π/₂ ; 0 ].
Et tan x – x – ^x3/₃ ≥ 0 sur [ 0 ; ^Π/₂ [.

Du coup, tan x ≤ x + ^x3/₃ sur ] –^Π/₂ ; 0 ].
Et tan x ≥ x + ^x3/₃ sur [ 0 ; ^Π/₂ [.

Donc ce n’est pas vrai pour les x positifs.

Bonne compréhension,
Sylvain Jeuland