Exercice de maths de seconde sur la géométrie dans l’espace avec un prisme droit, intersection, plan, droites parallèles, construction.
Exercice N°273 :
Soit ABCDEF, un prisme droit, I un point de ]DE[, J un point de ]DF[ et K, le centre de la face BCFE du prisme. On s’intéresse à l’intersection des plans (IJK) et (ABC).
1er cas : (IJ)//(EF)
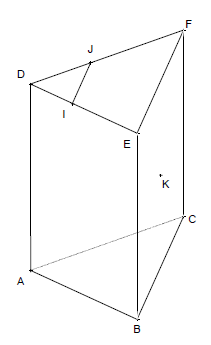
1) Montrer que l’intersection de (IJK) avec (BCF) est parallèle à (IJ). On appellera (D) cette intersection.
On appelle L l’intersection de (D) avec (EB) et M l’intersection de (D) avec (FC).
2) Construire sur le schéma l’intersection de (IJK) avec (ABC). On ne justifiera que l’existence des points supplémentaires nécessaire à la construction ou l’utilisation des propriétés sur le parallélisme.
2ème cas : (IJ) n’est pas parallèle à (EF).
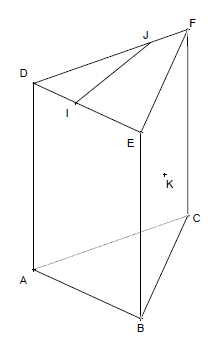
3) Sans justifier, construire sur le schéma l’intersection de (IJK) avec (BCF) puis de (IJK) avec (ABC).
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : prisme droit, géométrie, intersection.
Exercice précédent : Géométrie 3D – Pyramide, parallélogramme, intersections – Seconde

