Maths de terminale sur les fonctions. Exercice sur un bénéfice, polynôme, rationnelle, droite, coût, quantité, graphique, maximum, dérivée.
Exercice N°403 :
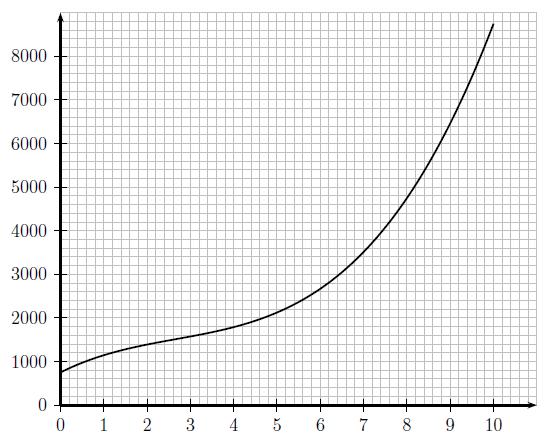
L’entreprise Sheddi produit du tissu en coton. Celui-ci est fabriqué en 1 mètre de large et pour une longueur x exprimée en kilomètre, x étant compris entre 0 et 10.
Le coût total de production en euros de l’entreprise Sheddi est donné en fonction de la longueur x par la formule
C(x) = 15x3 − 120x2 + 500x + 750.
Le graphique ci-dessus donne la représentation graphique de la fonction C.
Les deux parties A et B de cet exercice sont indépendantes.
Partie A : Étude du bénéfice
Si le marché offre un prix p en euros pour un kilomètre de ce tissu, alors la recette de l’entreprise Sheddi pour la vente d’une quantité x est égal à
R(x) = px.
1) Tracer sur le graphique la droite D1 d’équation
y = 400x.
Expliquer, au vu de ce tracé, pourquoi l’entreprise Sheddi ne peut pas réaliser un bénéfice si le prix p du marché est égal à 400 euros.
Dans cette question on suppose que le prix du marché est égal à 680 euros.
2) Tracer sur le graphique la droite D2 d’équation
y = 680x.
Déterminer graphiquement, avec la précision permise par le graphique, pour quelles
quantités produites et vendues, l’entreprise Sheddi réalise un bénéfice si le prix p du marché est de 680 euros.
On considère la fonction B définie sur l’intervalle [0 ; 10] par
B(x) = 680x − C(x).
3) Démontrer que pour tout x ∈ [0 ; 10] on a :
B ′ (x) = −45x2 + 240x + 180.
4) Étudier les variations de la fonction B sur [0 ; 10].
En déduire pour quelle quantité produite et vendue le bénéfice réalisé par l’entreprise Sheddi est maximum. Donner la valeur de ce bénéfice.
Partie B : Étude du coût moyen
On rappelle que le coût moyen de production CM mesure le coût par unité produite. On considère la fonction CM définie sur l’intervalle [0 ; 10] par
CM(x) = C(x)/x.
5) Démontrer que pour tout x appartenant à l’intervalle ]0 ; 10] on a :
CM ‘(x) = ( 30(x − 5) (x2 + x + 5) )/x2.
6) Démontrer que pour tout x ∈ ]0 ; 10],
CM ‘ (x) est du signe de (x − 5).
En déduire les variations de la fonction CM sur l’intervalle ]0 ; 10].
7) Pour quelle quantité de tissu produite le coût moyen de production est-il minimum?
Que valent dans ce cas le coût moyen de production et le coût total ?
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, bénéfice, polynôme, rationnelle.
Exercice précédent : Fonctions – Courbe représentative, signe, dérivée – Terminale

