Maths de terminale : exercice avec fonction, dérivée et courbe représentative à analyser. Tableau de signe, pente, inéquation et primitive.
Exercice N°402 :
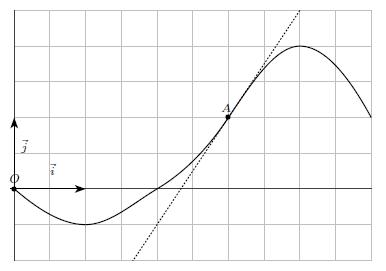
Le plan est muni d’un repère orthonormé (O ; →i ; →j).
La courbe Cf (en traits pleins) représente une fonction f définie et dérivable sur l’intervalle [0 ; 5].
La droite T (en pointillés) est la tangente à Cf au point A(3 ; 1).
La fonction F est définie et dérivable sur [0 ; 5], de dérivée f.
Elle vérifie F(2) = 0.
On note CF sa courbe représentative dans un repère orthonormé.
1) Donner f(1) sans justifier.
2) Résoudre f(x) > 0 sans justifier.
3) Déterminer f ‘ (3) en justifiant.
4) Dresser le tableau de signes de f ‘ en justifiant.
5) Donner le tableau de variations de F en justifiant.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, fonction, dérivée, courbe.
Exercice précédent : Dérivation – Calculs, polynômes et rationnelles – Première

