Maths sur les fonctions avec un polynôme, exercice, convexité, terminale, coût, fixe, marginal, point d’inflexion, lecture graphique.
Exercice N°407 :
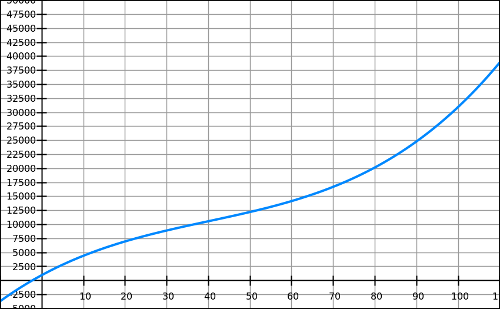
Dans une entreprise, le coût total, en euros, pour la fabrication de machines est modélisé par la fonction définie sur l’intervalle [0 ; 100] par l’expression :
C(q)= 0.05q3 – 6q2 + 400q + 1000.
La fonction C est représentée par la courbe ci-dessus dans un repère orthogonal.
1) Quels sont les coûts fixes de production ?
2) Par lecture graphique, indiquer la production pour laquelle le coût total est supérieur à 16000.
3) Étudier la convexité de la fonction C.
4) Montrer que la courbe admet un point d’inflexion.
5) Tracer la tangente correspondante après avoir déterminé son équation.
6) Expliquer comment lire graphiquement la production pour laquelle le coût marginal est minimal.
7) Calculer le coût marginal Cm en fonction de q.
8) Étudier les variations de la fonction Cm.
9) En déduire la valeur pour laquelle le coût marginal est minimal.
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre Continuité et Convexité de Terminale (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Exercice précédent : Fonctions – Lecture graphique, convexité, coût moyen – Terminale

