Maths de terminale: exercice d’exponentielle avec variation, courbe représentative, dérivée, signe, croissance, décroissance, limite.
Exercice N°276 :
Soit f une fonction dérivable sur R dont le tableau de variations est donné ci-contre où a et b désignent deux réels.
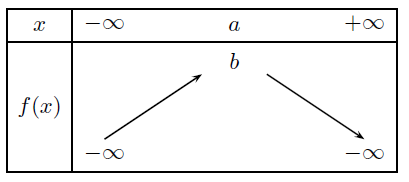
1) Déterminer le signe de f ‘ (x) selon les valeurs de x.
Dans le plan muni d’un repère orthonormé (O, →i, →j), on a tracé deux courbes C1 et C2.
Elles coupent l’axe des ordonnées aux points A et B
d’ordonnées −2 et 1/2 respectivement.
L’une de ces courbes est la courbe représentative de la fonction dérivée f ‘ de f.
L’autre est la courbe représentative d’une fonction F sur R, telle que F ‘ = f.
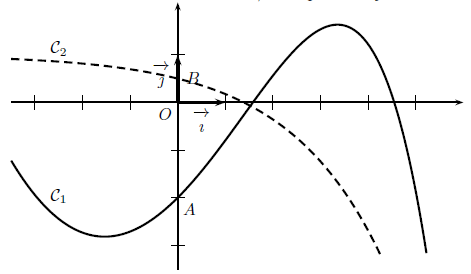
2) Indiquer laquelle de ces deux courbes est la courbe représentative de la fonction f ‘. Justifier la réponse.
3) A l’aide des courbes C1 et C2, prouver que
1 < a < 2
et
b > 0.
La fonction F a pour expression :
F(x) = (1/2)x2 + 2x − 2e(x/2).
4) Déterminer l’expression de f, et démontrer que
f ‘ (x) = 1 − (1/2)e(x/2).
5) Justifier alors le tableau de variations de f, en précisant les valeurs exactes de a et b, et en justifiant les limites de f en −∞ et +∞.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, exponentielle, variation, courbe.
Exercice précédent : Exponentielle – Equation, dérivée, limite, variation – Terminale

