Essaie les exercices de DS, clique ci-dessous
Maths de terminale : exercice de suite avec récurrence, limite. Arithmétique, géométrique, premier terme, démonstration, égalité.
Exercice N°409 :
Exercice N°409 :
Soit un la suite définie par
{ u0 = 1 ;
{ un+1 = un + 2n + 3.
1) Calculer u1, u2 et u3. Lis la suite »
Exercice de maths de première sur l’algorithme et suite arithmétique et suite géométrique. Forme récurrente et explicite.
Exercice N°134 :
Le gérant d’un parc d’attractions note chaque année le nombre de visiteurs. Il obtient les résultats suivants:
On note u0 le nombre de visiteurs en 2015, u1 le nombre de visiteurs en 2016 et u2 le nombre de visiteurs en 2017.
1) Les nombres u0, u1 et u2 forment-ils une suite arithmétique? Lis la suite »
Exercice de maths de première sur l’algorithme de second degré avec si, alors, conditions, sinon. Variables et calcul, affectations.
Exercice N°036 :
On considère l’équation du second degré suivante :
mx2 – p = 0.
Voici un algorithme permettant de résoudre cette équation en fonction des paramètres m et p.
1) Compléter les pointillés de cet algorithme. Lis la suite »
Maths : exercice avec suite arithmétique de terminale. Fonction, sens de variation, courbe, graphique, convergence, croissance, limite.
Exercice N°410 :
Soit f la fonction définie sur [0 ; 2] par
f(x)= (x − 4)/(x − 3).
1) Étudier les variations de f. En déduire que pour tout x ∈ [0 ; 2],
f(x) ∈ [0 ; 2]. Lis la suite »
Maths de première : exercice de limites de suites avec convergence. Fractions, racines carrées, polynômes, minorée, bornée, croissante.
Exercice N°408 :
Exercice N°408 :
1-2-3-4) Calculer la limite des suites suivantes :
1) tn = (n2 + 3n + 1)/(3n – n2). Lis la suite »
Exercice : Clic droit vers l’exercice
Tout le corrigé :
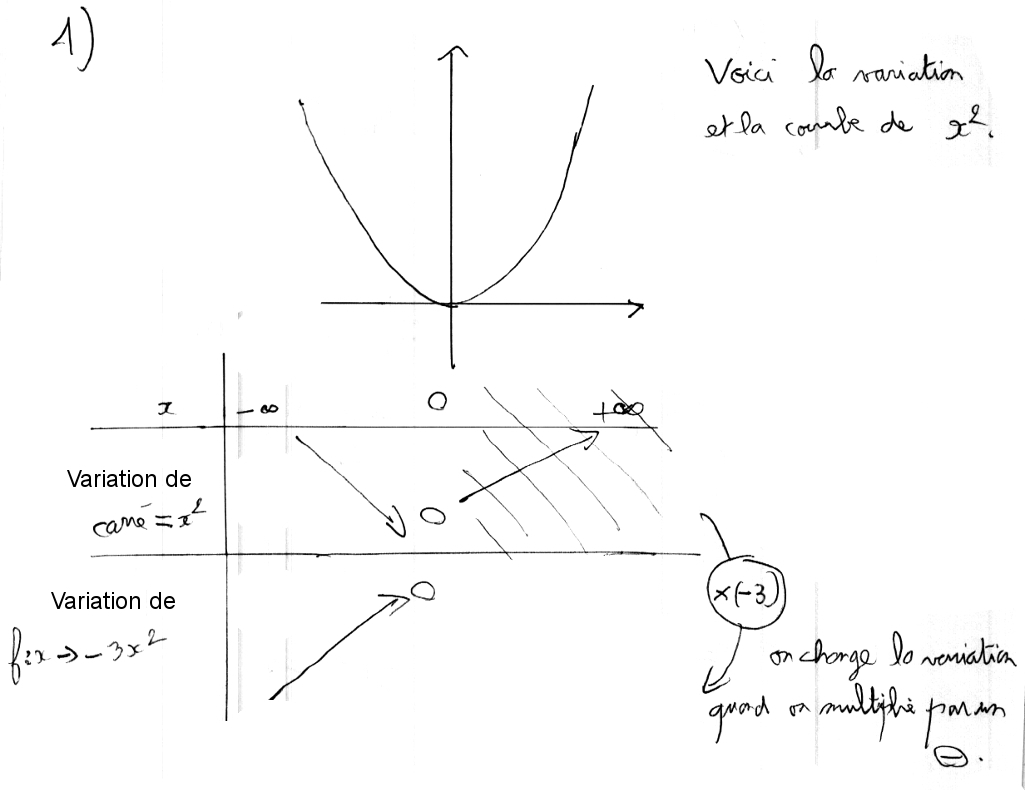
1) Montrer que f de formule
f : x → 1/(3x2 + 4)
est strictement croissante sur [−2 ; 0] et strictement décroissante sur [0 ; 2] :
Rédaction :
Je commence sur [−2 ; 0].
On prend -2 ≤ a < b ≤ 0 car on est sur [−2 ; 0]. Je prends en compte les bornes de l’intervalle qui vont me donner des informations.
-2 ≤ a < b ≤ 0
⇔ (-2)2 ≥ a2 > b2 ≥ 02
(on change le sens des inégalités
car la fonction « carré » est décroissante sur [−2 ; 0])
⇔ 3×4 ≥ 3×a2 > 3×b2 ≥ 3×0
(on garde le sens des inégalités quand on multiplie (ou divise) par un nombre positif, ici 3)
⇔ 12 + 4 ≥ 3×a2 + 4 > 3×b2 + 4 ≥ 0 + 4
(on garde le sens des inégalités car on ajoute (ou soustrait) un nombre)
⇔ 1/16 ≤ 1/(3×a2 + 4) < 1/(3×b2 + 4) ≤ 1/4
(on change le sens des inégalités car la fonction « inverse » est strictement décroissante sur [−2 ; 0])
⇔ 1/16 ≤ f(a) < f(b) ≤ 1/4
a < b donne f(a) < f(b) donc f est strictement croissante sur [−2 ; 0].
De même, sur [0 ; 2] :
On prend -2 ≤ a < b ≤ 0 car on est sur [0 ; 2]. Je prends en compte les bornes de l’intervalle qui vont me donner des informations.
-2 ≤ a < b ≤ 0
⇔ 02 ≥ a2 < b2 ≥ 22
(on garde le sens des inégalités car la fonction « carré » est croissante sur [0 ; 2])
⇔ 3×0 ≤ 3×a2 < 3×b2 ≤ 3×4
(on garde le sens des inégalités quand on multiplie (ou divise) par un nombre positif, ici 3)
⇔ 0 + 4 ≤ 3×a2 + 4 < 3×b2 + 4 ≤ 12 + 4
(on garde le sens des inégalités car on ajoute (ou soustrait) un nombre)
⇔ 1/4 ≥ 1/(3×a2 + 4) > 1/(3×b2 + 4) ≥ 1/16
(on change le sens des inégalités car la fonction « inverse » est strictement décroissante sur [0 ; 2])
⇔ 1/4 ≥ f(a) > f(b) ≥ 1/16
a < b donne f(a) > f(b) donc f est strictement décroissante sur [0 ; 2].
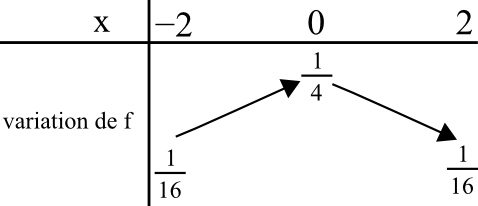
Pour résumer, voici le tableau de variation de la fonction f :
2) Tableau de variations de g sur [−2 ; 2] avec
g(x) = − √f(x) + 1/2 :
Rédaction :
On peut rédiger de la même manière avec
a < b donne f(a) < f(b) ou f(a) > f(b)
mais je vais choisir la méthode des tableaux de variation.
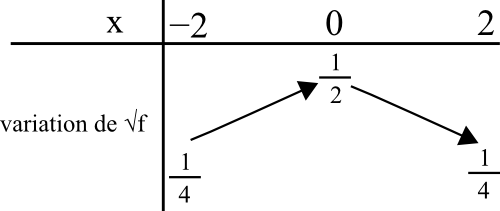
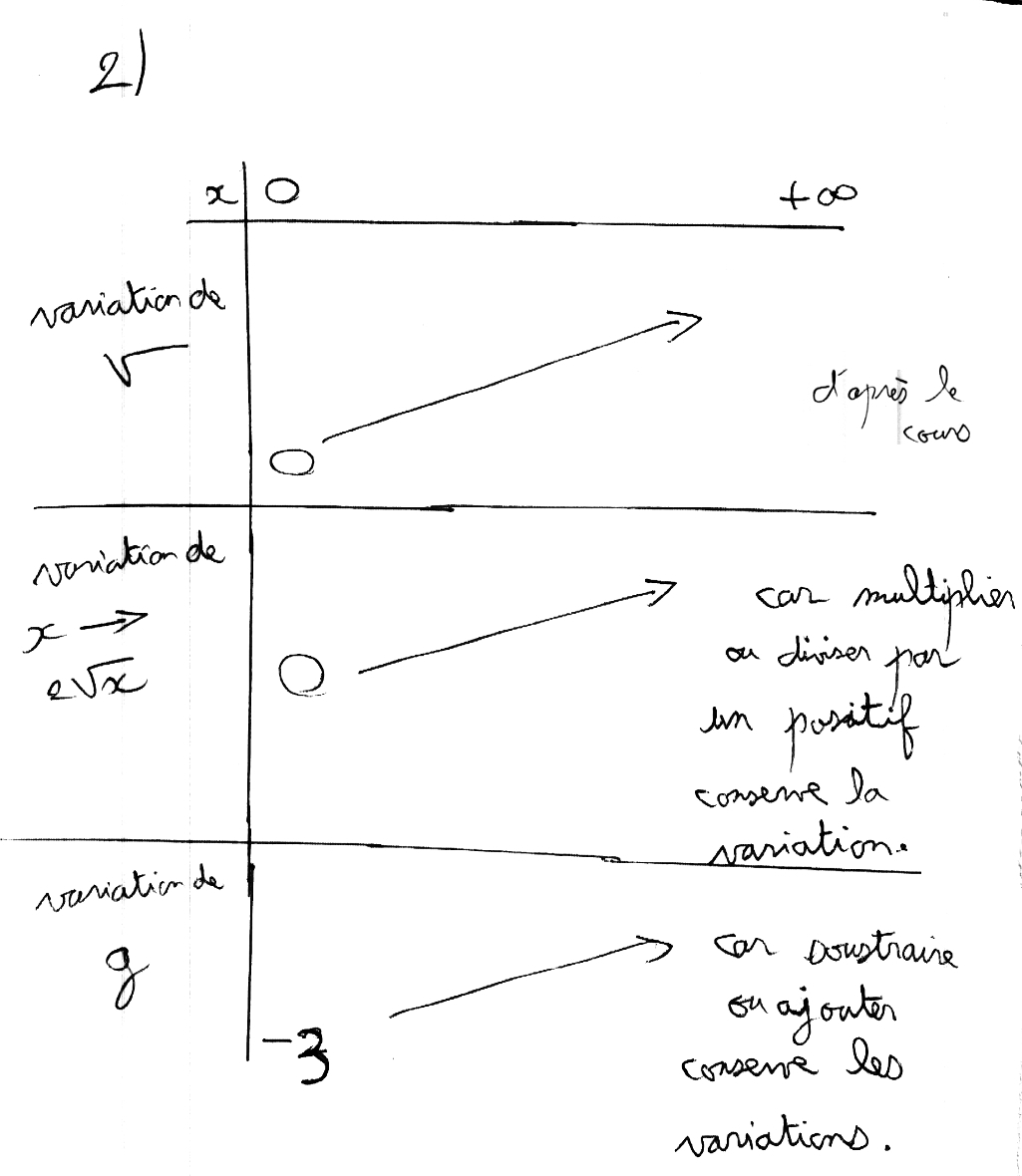
Je reprends le tableau de variation de f et je lui applique la fonction « racine » car f(x) subit l’effet de la racine en premier lieu.
Les valeurs des fractions sont mises à la racine. Les 1 restent 1, 16 devient 4 et 4 devient 2.
Les variations ne changent pas car la fonction « racine » est strictement croissante sur R+.
On note que les contenus de la racine sont positifs : 1/4 et 1/16.
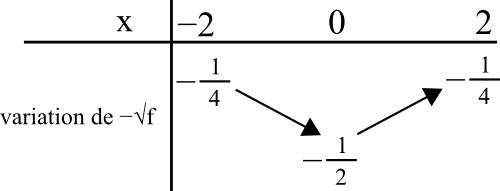
En second lieu, le nombre √f(x) est multiplié par (-1) en témoigne le « moins » devant lui. Comme on multiplie par un nombre négatif, les variations changent et les images sont aussi multipliées par (-1). Cela donne le tableau :
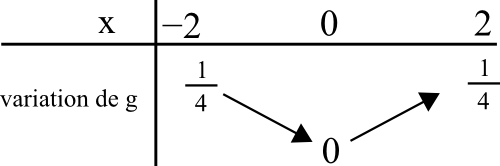
Enfin pour obtenir la fonction g, on ajoute 1/2 à l’ensemble. Comme on ajoute un nombre, les variations ne changent pas. Seules les valeurs se voient augmentées de 1/2 ci-dessous :
3) Encadrement de g(x) sur [−2 ; 2] :
On voit d’après la tableau de signe que
0 ≤ g(x) ≤ 1/4.
Il a été utile de calculer toutes les images des bornes des intervalles.
Bonne compréhension,
Sylvain Jeuland
Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) f : x → -3x2 sur ]-∞ ; 0] :
Rédaction de la méthode 1 :
On prend a < b ≤ 0 car on est sur ]-∞ ; 0].
a < b ≤ 0
⇔ a2 > b2 ≥ 02
(on change le sens des inégalités car la fonction « carré » est strictement décroissante sur ]-∞ ; 0])
⇔ -3a2 < -3b2 ≤ -3×0
(on change le sens des inégalités car on multiplie par un nombre négatif)
⇔ f(a) < f(b) ≤ 0
a < b donne f(a) < f(b) donc f est strictement croissante sur ]-∞ ; 0].
Rédaction de la méthode 2 :
2) g : x → 2√(x) – 3 sur [0 ; +∞[ :
Rédaction de la méthode 1 :
On prend 0 ≤ a < b car on est sur [0 ; +∞[.
0 ≤ a < b
⇔ √(0) < √(a) ≤ √(b)
(on garde le sens des inégalités car la fonction « racine » est strictement croissante sur [0 ; +∞[)
⇔ 2√(0) < 2√(a) ≤ 2√(b)
(on garde le sens des inégalités car on multiplie par un nombre positif, ici 2)
⇔ 0 – 3 < 2√(a) – 3 ≤ 2√(b) – 3
(on garde le sens des inégalités quand on ajoute ou on soustrait)
-3 < f(a) ≤ f(b)
a < b donne f(a) < f(b) donc f est strictement croissante sur [0 ; +∞[.
Rédaction de la méthode 2 :
3) h : x → 1/|x| sur R* :
Rédaction de la méthode 2 uniquement :
La fonction que l’on a là est l’inverse de la fonction absolue. Donc je représente les variations de la fonction « valeur absolue » ci-dessous.
D’après le cours, on obtient la première ligne :
Comme la fonction « inverse » est strictement décroissante sur R– et sur R+. On change le sens des variations de la valeur absolue pour obtenir celles de h ci-dessus.
4) l : x → -1 + ( 1/(2x + 4) ) sur ]-2 ; +∞[ :
Rédaction de la méthode 1 :
On prend 0 ≤ a < b car on est sur [-2 ; +∞[.
-2 ≤ a < b
⇔ 2×(-2) < 2a ≤ 2b
(on garde le sens des inégalités car on multiplie par un nombre positif, ici 2)
⇔ -4 + 4 < 2a + 4 ≤ 2b + 4
(on garde le sens des inégalités quand on ajoute ou on soustrait)
⇔ 0 < 2a + 4 ≤ 2b + 4
(ici on a zéro à gauche, la partie gauche va disparaître quand on va passer à l’inverse)
⇔ 1/(2a + 4) ≥ 1/(2b + 4)
(on change le sens des inégalités car la fonction « inverse » est strictement décroissante sur ]0 ; +∞[. Ici on s’aperçoit que nos valeurs sont strictement au-dessus de zéro)
⇔ -1 + 1/(2a + 4) ≥ -1 + 1/(2b + 4)
(on garde le sens des inégalités quand on ajoute ou on soustrait)
⇔ f(a) ≥ f(b)
a < b donne f(a) > f(b) donc f est strictement décroissante sur [-2 ; +∞[.
Rédaction de la méthode 2 :
Bonne compréhension,
Sylvain Jeuland
Maths de première : exercice de dérivée avec lecture graphique. Courbe, coefficient directeur, équation de la tangente, inéquation.
Exercice de lecture graphique à trouver et à changer.
Exercice N°044 :
Voici la courbe représentative Cf d’une fonction f définie sur R.
1) D’après le graphique, donner la valeur de f ‘ (-4) en justifiant ;
puis f ‘ (-5), f ‘ (-2) et f ‘ (4). Lis la suite »
Maths de première sur l’étude d’une fonction. Exercice de dérivation avec tangente parallèle. Variation, équation, courbe dans un repère.
Exercice N°042 :
Exercice N°042 :
On considère la fonction f définie sur R par :
f(x) = 2 – 2(1 – x)/(x2 + 1)
On note Cf sa courbe représentative.
1) Calculer f ‘ (x).
Vérifier que f ‘ (x) = -2(x2 – 2x – 1)/(x2 + 1)2 . Lis la suite »
Maths de première : exercice avec inéquation, valeur absolue. Inverse, courbe, fonctions affines, équations, droite, racine, expression.
Exercice N°606 :
Les questions de 1) à 5) font partie d’un QCM.
1) La fonction x → | 1/(1 − x) | :
a) est strictement croissante sur ] −∞ ; 1 [, Lis la suite »
