Maths de première : exercice avec inéquation, valeur absolue. Inverse, courbe, fonctions affines, équations, droite, racine, expression.
Exercice N°606 :
Les questions de 1) à 5) font partie d’un QCM.
1) La fonction x → | 1/(1 − x) | :
a) est strictement croissante sur ] −∞ ; 1 [,
b) est strictement décroissante sur ] −∞ ; 1 [,
c) n’est pas monotone sur ] −∞ ; 1 [.
2) Soit a un réel strictement positif.
Dire que x ∈ [ 1 − a ; 1 + a ] signifie :
a) |x| ≤ 1 + a,
b) |x − 1| ≤ a,
c) |x − a| ≤ 1.
3) Si x est un réel de l’intervalle ] 0 ; 1 [, alors :
a) |x2 − x| > |x2 − √x|,
b) |x2 − x| < |x2 − √x|,
c) √( (x − 1)2 ) = x − 1.
4) Si a et b sont deux réels non nuls de signes opposés, alors :
a) |a − b| = |a| + |b|,
b) |a − b| = |a| − |b|,
c) |a + b| = |a| + |b|.
5) Combien de nombres entiers relatifs k sont solutions de l’inéquation
| k − √2 | ≤ 3 ?
a) 3,
b) 5,
c) 6.
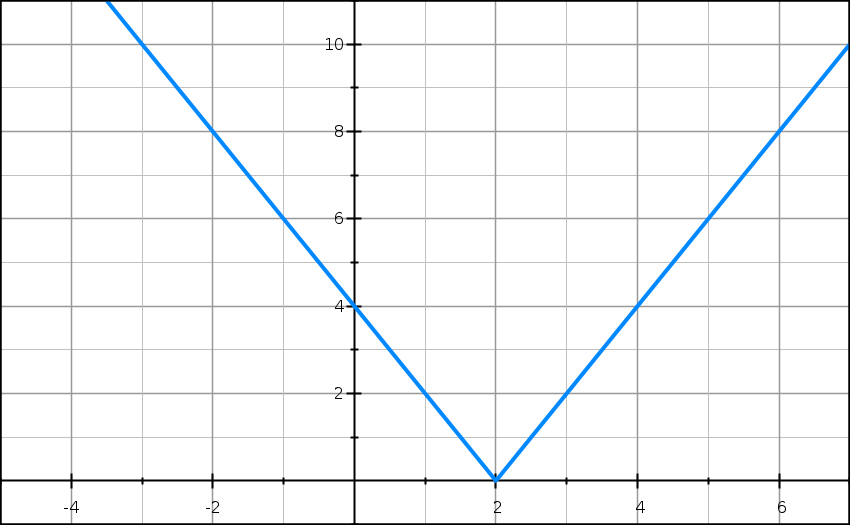
On considère une fonction g définie sur R dont la courbe dans un repère orthonormé est donnée en haut de l’exercice.
6) Donner l’équation réduite de la droite passant par A(0 ; 4).
7) Donner l’équation réduite de la droite passant par B(4 ; 4).
8) Donner une expression de g(x) à l’aide d’une valeur absolue.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, inéquation, valeur absolue.
Exercice précédent : Valeur absolues – Équations, inéquations, fonction – Première

