Maths : exercice de factorisation et équation de seconde. Calcul, développement, réduction, fraction, racine carré, équation.
Exercice N°039 :
Exercice N°039 :
On considère A = (3x – 2)2 – 252.
1) Développer et réduire A. Lis la suite »
Exercice sur les vecteurs avec parallélogramme de première. Maths, relations vectorielles, appartenance à une droite, colinéarité, égalités.
Exercice N°597 :
Exercice N°597 :
ABCD est un parallélogramme. Les points I et K sont les milieux respectifs de [AB] et [CD].
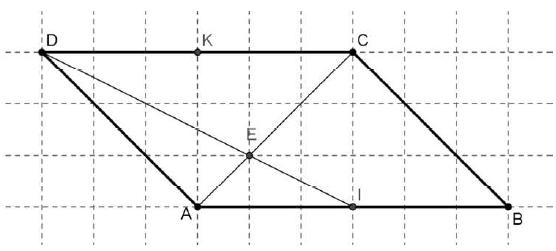
1) Exprimer le vecteur →DI en fonction de →AB et →AD. Lis la suite »
Exercice de maths de statistiques de seconde. Intervalle, moyenne, écart-type, médiane, premier et troisième quartiles, pourcentages.
Exercice N°755 :
Exercice N°755 :
Lors d’un contrôle de fabrication sur un lot de résistances, un technicien a obtenu les résultats suivants regroupés dans le tableau statistique ci-dessous :
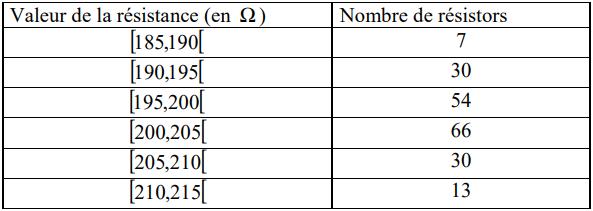
1) Déterminer le nombre total de résistances contrôlés. Lis la suite »
Exercice sur un intervalle et inégalité de maths de seconde, plus grand, plus petit, égal, crochets, axe des abscisses, réels, nombre
Exercice N°574 :
Exercice N°574 :
Pour chaque inégalité, écrire à l’aide d’intervalles les ensembles de réels x vérifiant les inégalités suivantes. Tracer l’axe des abscisses en entourant le ou les bon(s) intervalles(s).
1) L’inégalité est :
1 < x ≤ 3
donc l’intervalle I = ? Lis la suite »
Trigonométrie – Équations, inéquation, sin, cos – Première
6 octobre 2021
Maths de première : exercice d’équations avec sinus et cosinus. Trigonométrie, égalité, inégalité, polynôme, cercle à tracer.
Exercice N°035 :
Exercice N°035 :
1) Résoudre dans l’intervalle ]-π ; π ] l’équation trigonométrique « sinus » suivante
sin x = –√2/2
en détaillant soigneusement les étapes. Lis la suite »
Maths de première sur les suites : exercice de somme géométrique, arithmétique. Formules de cours et démonstrations d’égalités.
Exercice N°008 :
Exercice N°008 :
Soient (un) et vn) définis pour tout entier naturel, par :
un = (1/4)(2n + 4n – 5)
et
vn = (1/4)(2n – 4n + 5)
1) Calculer u0, u1, v0 et v1. Lis la suite »
Maths de seconde : exercice de fonction avec résolution graphique d’équations, tableau de valeurs, calculs d’image et d’antécédent.
Exercice N°030 :
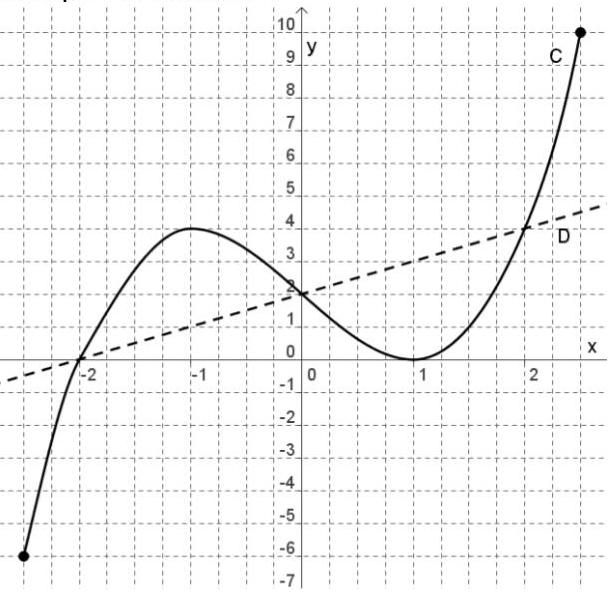
Soit f une fonction définie sur [-2,5 ; 2,5] représentée par la courbe C.
Soit g une fonction définie sur [-2,5 ; 2,5] représentée par la courbe D.
1) Déterminer les images par f de -2,5 ; -1,5 ; de 0 et de 2. Lis la suite »
Statistiques – Moyenne, variance, écart-type, pourcentage – Seconde
30 septembre 2021
Exercice sur la moyenne et la variance de seconde. Maths, statistiques, écart-type, tableau, valeurs, effectifs, pourcentage, intervalle.
Exercice N°753 :
Exercice N°753 :
La qualité de la rédaction, la clarté et la présentation des raisonnements sont importantes.
L’usage de la calculatrice est autorisé et les résultats seront arrondis à 10−2
près.
Vincent, le boulanger bio près de Vitré fait des petits pains appelés « alouettes ».
Le poids théorique d’une petite alouette est de 125 grammes. Voici la production du jour de Vincent :
1) Calculer la moyenne –x des masses des petites alouettes. Lis la suite »
Fonctions – Bases, limites, variations, équations – Terminale
30 septembre 2021
Maths de terminale : exercice, fonction, continuité, limite, variation, équation, théorème des valeurs intermédiaires, tableau de signe.
Exercice N°243 :
Exercice N°243 :
Soit f la fonction rationnelle définie sur Df = ]-∞ ; 2[ ⋃ ]2 ; +∞[
par
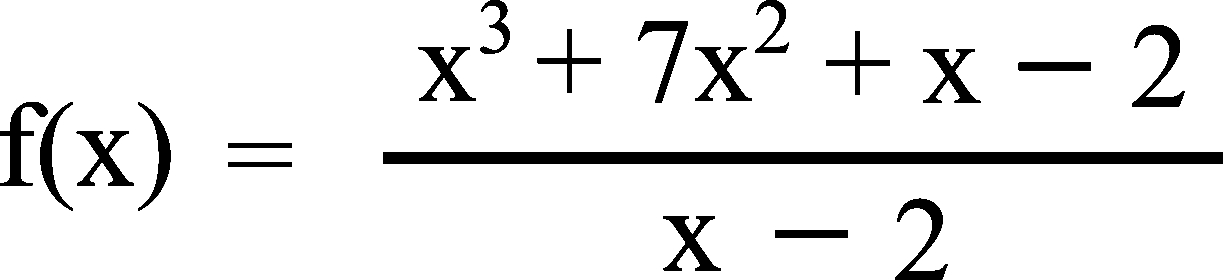
1) Étudier les limites aux bornes du domaine de définition Df et donner ses asymptotes éventuelles. Lis la suite »
Exercice de maths de terminale sur le bac 2016 sur la fonction, intégrale, primitive, logarithme népérien, dérivée, variation, TVI, surface.
Exercice N°600 :
Exercice N°600 :
La courbe (C) ci-dessous représente, dans un repère orthonormé, une fonction f définie et dérivable sur [0.5 ; 6]. Les points A(1 ; 3) et B d’abscisse 1,5 sont sur la courbe (C).
Les tangentes à la courbe (C) aux points A et B sont aussi représentées en pointillés sur ce graphique, la tangente au point B est horizontale.
On note f ‘ la fonction dérivée de f.
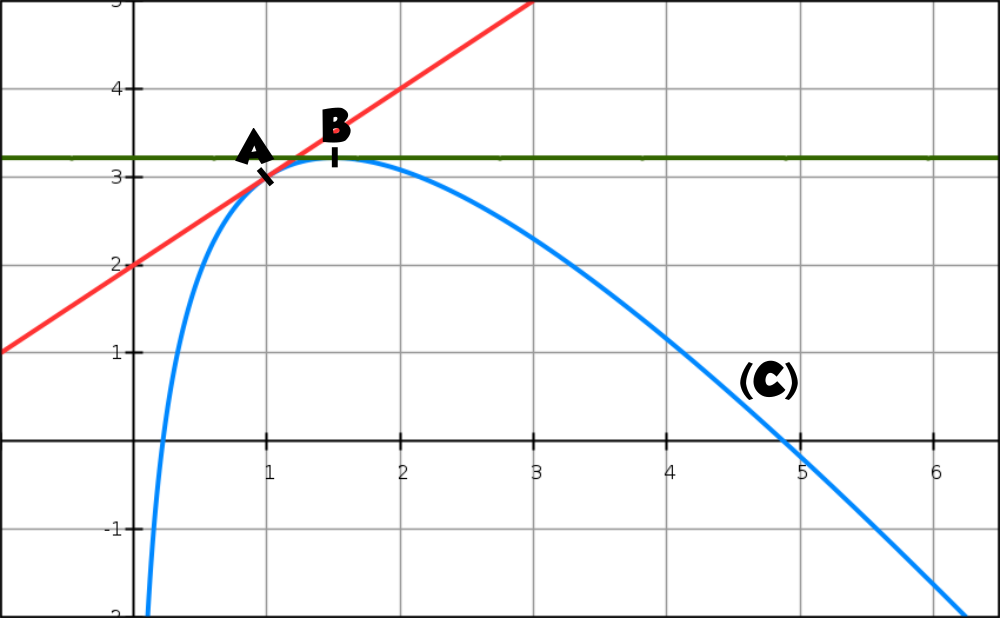
Les parties A et B sont indépendantes.
Partie A : Étude graphique
1) Déterminer f ‘ (1,5). Lis la suite »
