Exercice de maths de statistiques de seconde. Intervalle, moyenne, écart-type, médiane, premier et troisième quartiles, pourcentages.
Exercice N°755 :

Exercice N°755 :
Lors d’un contrôle de fabrication sur un lot de résistances, un technicien a obtenu les résultats suivants regroupés dans le tableau statistique ci-dessous :
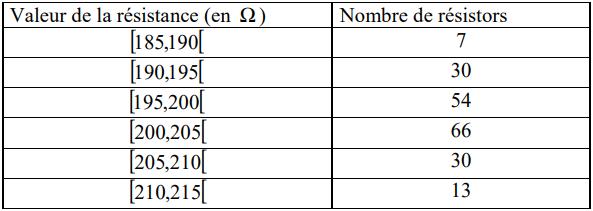
1) Déterminer le nombre total de résistances contrôlés.
2) Calculer la moyenne x– et l’écart type σ de cette série statistique. Les résultats seront arrondis à l’unité.
3) Le fabricant certifie qu’au moins 85 % des valeurs des résistances sont dans l’intervalle [190 ; 210[. Montrer par le calcul que cette affirmation est vérifiée.
4) Tracer le polygone des effectifs cumulés croissants d’unité graphique 2 cm pour 5 Ω et 1 cm pour 20 résistances.
5) Déterminer graphiquement la médiane Me de cette série statistique. Le résultat sera arrondi à l’unité et les traits de construction devront apparaître sur le schéma.
6) Interpréter la valeur de la médiane Me dans le contexte de l’exercice.
7) Calculer –x – σ et –x + σ.
8) À l’aide du graphique, estimer le nombre de resistances dont la valeur de la résistance est dans l’intervalle [ –x – σ ; –x + σ ]. Faire apparaître les traits du traçage sur le graphique.
9) À partir du résultat précédent, calculer le pourcentage de résistances dont la valeur de la résistance est dans l’intervalle [ –x – σ ; –x + σ ].
10) La valeur de la résistance est jugée satisfaisante si au moins 65% des résistances ont une valeur de résistance dans l’intervalle [ –x – σ ; –x + σ ]. Est-ce le cas ?
11) Déterminer graphiquement les quartile Q1 et quartile Q3 de cette série statistique. Les résultats seront arrondis à l’unité et les traits de construction devront apparaître sur le schéma.
12) Interpréter les valeurs des quartiles Q1 et quartile Q3 dans le contexte de l’exercice.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : intervalle, moyenne, écart-type.
Exercice précédent : Statistiques – Variance, écart-type, intervalle, histogramme – Seconde

