frenchmaths.com (par Sylvain Jeuland)

Exercice de maths sur fonction dérivée, exponentielle, première, inéquations, coûts marginal, moyen, total, équation, coût, marginal, moyen.

Exercice N°331 :

On s’intéresse à la production mensuelle d’une certaine catégorie d’articles pour une entreprise. On sait que le nombre d’articles produits par mois est compris entre 0 et 500.
On suppose que le coût total, exprimé en milliers d’euros, peut être modélisé par la fonction C_T définie sur l’intervalle [0 ; 5] par
C_T(x) = 2x² + xe^{-2x + 3},
où x est exprimé en centaines d’articles.

1) Déterminer la fonction coût marginal C_m, c’est-à-dire la fonction dérivée de la fonction coût total C_T.

2) Calculer le coût marginal pour la fabrication de 150 articles.

La fonction coût moyen, notée C_M est la fonction définie sur ]0 ; 5] par
C_M(x) = ^C_T(x)/_x.

3) Donner une expression de C_M(x) en fonction de x.

4) Déterminer C ‘_M(x) où C ‘_M désigne la fonction dérivée de C_M.

5) Résoudre dans R l’équation 1 – e^{-2x + 3} = 0.

6) Résoudre dans R l’équation 1 – e^{-2x + 3} > 0.

7) En déduire le sens de variation de C_M sur ]0 ; 5[.

8) Pour quelle production q l’entreprise a-t-elle un coût moyen minimal et quel est ce coût ?

Chaque centaine d’articles est vendue 7000 €. La recette totale pour x centaines d’articles est donnée, en admettant que toute la production soit vendue, par
R(x) = 7x
en milliers d’euros.
Le bénéfice est donc défini par
B(x) = R(x) − C_T(x).

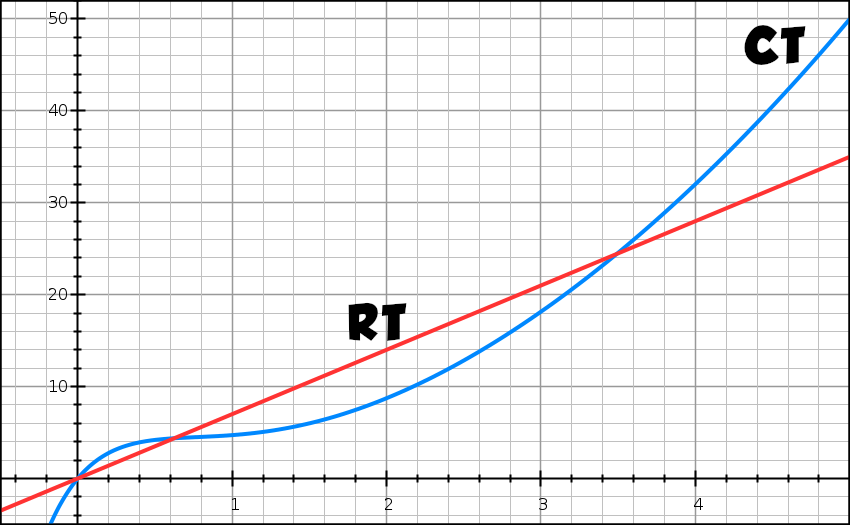
Ci-haut sont représentées les fonctions C_T et R (avec la droite R_T).

Par lecture graphique déterminer :

9) – l’intervalle sur lequel le rendement marginal est croissant (ce qui signifie que le coût marginal est décroissant),

10) – le coût moyen minimal (ne pas faire cette question, je ne vois pas comment c’est possible de le trouver dans cet exercice)

11) – l’intervalle dans lequel doit se situer la production x pour qu’il y ait un bénéfice positif de l’entreprise E,

12) – la production x₀ pour laquelle le bénéfice est maximal. On fera apparaître les constructions nécessaires.

13) Avec l’aide de votre calculatrice, affiner l’intervalle (à un article près) dans lequel doit se situer la production x pour qu’il y ait un bénéfice positif de l’entreprise E.

Bon courage,
Sylvain Jeuland

Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :

Pour avoir tous les corrigés actuels de Première de ce chapitre Exponentielle (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :

77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.

Mots-clés de l’exercice : dérivée, exponentielle, première, inéquations.

Exercice précédent : Statistiques – Tableau, moyenne, écart-type, pourcentage – Première