frenchmaths.com (par Sylvain Jeuland)

Maths de terminale : exercice, intégrale, fonction, suite. Primitive, exponentielle, croissance,, variation, conjecture, limite, convergence.

Exercice N°424 :

On désigne par (I_n) la suite définie pour tout entier n supérieur ou égal à 1 par :

I_n = ∫_{[de 0 à 1]} xⁿe^−xdx

1) Montrer que
xe^−x = e^−x − (xe^−x)′
pour tout x ∈ R ;
puis calculer I₁.

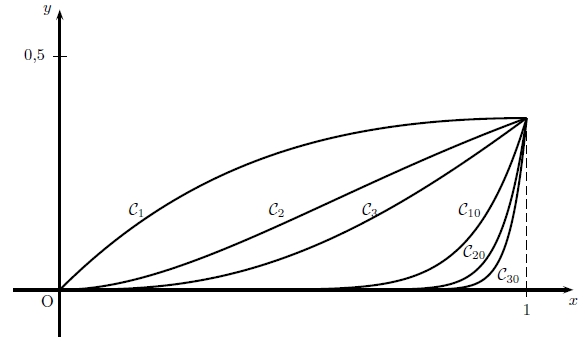
Sur le graphique ci-dessus, on a représenté les portions des courbes C₁, C₂, C₃, C₁₀, C₂₀, C₃₀ comprises dans la bande définie par 0 ≤ x ≤ 1. Ces courbes C_n représentent les fonctions d’expression f_n(x) = xⁿe^−x.

2) Formuler une conjecture sur le sens de variation de la suite (I_n) en décrivant votre démarche. Pouvez-vous aussi conjecturer la limite de (I_n) ?

3) Montrer que pour tout n supérieur ou égal à 1, on a
(I_n) ≥ 0.

4) Montrer que (I_n) est décroissante et conclure quant à la convergence de (I_n).

5) Montrer que pour tout x ∈ [0 ; 1] on a :
xⁿe^−x ≤ xⁿ.

6) En déduire un encadrement de (I_n) et déterminer
lim_n→+∞(I_n).

Bon courage,
Sylvain Jeuland

Question 1 : Clic droit vers le corrigé

Pour avoir la suite du corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :

Pour avoir tous les corrigés actuels du second degré (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :

77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.

Mots-clés de l’exercice : exercice, intégrale, fonction, suite.

Exercice précédent : Logarithme Népérien – Quotient, bénéfice, maximum – Terminale