Maths de première : exercice d’équations de cercles avec tangentes, coefficients directeurs, vecteurs directeurs, coordonnées de points.
Exercice N°784 :

Exercice N°784 :
Voici ci-dessous un petit Python sous forme de logo pour les feuilles d’exercices de programmation. Les points A, B, C, D, M, N et P sont à coordonnées entières.
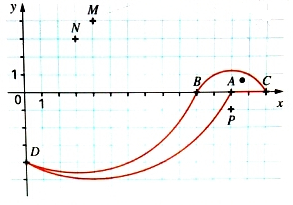
1) Lire les coordonnées des points A, B, C, D, M, N et P.
2) Déterminer une équation du cercle ΓM de centre M passant par A et D.
3) Déterminer une équation du cercle ΓN de centre N passant par B et D.
4) Déterminer une équation du cercle ΓP de centre P passant par B et C.
Le logo donne une impression de “cassure” au niveau du point B.
L’objectif des questions suivantes est de trouver des coordonnées du point P qui permettent de lisser la courbe à cet endroit.
Pour cela, il est nécessaire et il suffit que la tangente du cercle ΓN en B ait le même coefficient directeur que la tangente du cercle ΓP en B.
5) Déterminer les coordonnées du vecteur →NB.
6) En déduire les coordonnées de →n, un vecteur directeur de la tangente à ΓN en B.
Soit (12 ; yP) les coordonnées de P.
7) Calculer les coordonnées de →BP et en déduire la valeur de yP qui permet d’avoir des tangentes de même coefficient directeur pour éviter la “cassure” au niveau du point B.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, équations, cercles, tangentes .
Exercice précédent : Géométrie – Équations cartésiennes, droite perpendiculaire – Première

