Maths de seconde : exercice avec fonctions, équations, inéquations. Résolutions graphiques et par calcul. Polynôme du second degré et droite.
Exercice N°046 :
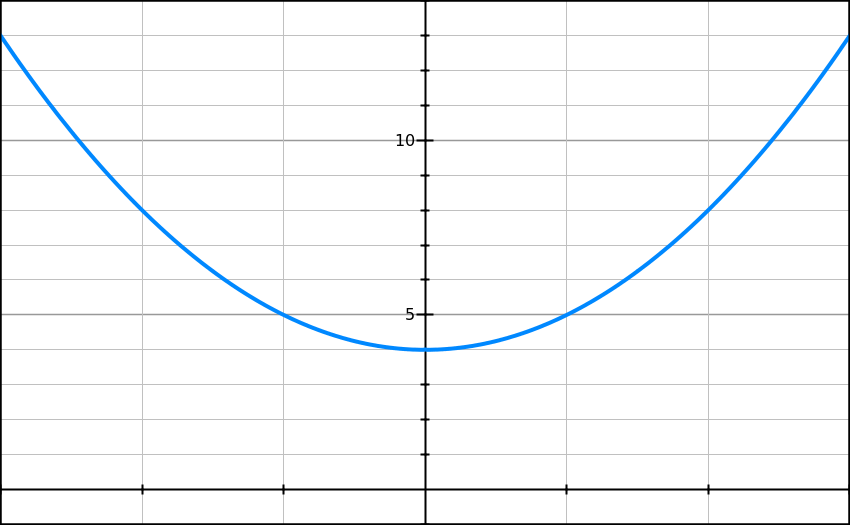
0) Démontrer que la fonction h représentée ci-dessus :
x → x2 + 4
est croissante sur [0 ; +∞ [.
On considère le fonctions f et g définies par
f(x) = (1/2) x2
et
g(x) = 3x – 4.
1) Représenter dans un autre et même repère les courbes Cf et Cg des fonctions f et g sur l’intervalle [-4 ; 6].
Échelle : 1 cm pour 1 unité en abscisses, 1 cm pour 2 unités en ordonnées.
2) Résoudre graphiquement l’équation f(x) = g(x).
Indiquer sur le graphique les marques de la lecture graphique et répondre sur la feuille ou le cahier.
3) Montrer que pour tout réel x,
(1/2) x2 – 3x + 4 = (1/2) (x – 2)(x – 4).
4) En déduire la résolution algébrique (par le calcul) de l’équation f(x) = g(x).
5) A l’aide des courbes représentatives des fonctions f et g, résoudre l’inéquation
f(x) ≤ g(x).
6) Résoudre maintenant par le calcul l’inéquation
f(x) ≤ g(x).
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de Seconde de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés pour cet exercice : exercice, fonctions, équations, inéquations.
Exercice précédent : Dérivation – Fonctions, intervalles et Variations – Première

