Maths de première : exercice de dérivation avec optimisation de surface. Second degré, signe, variation, maximum, minimum, trigonométrie.
Exercice N°056 :
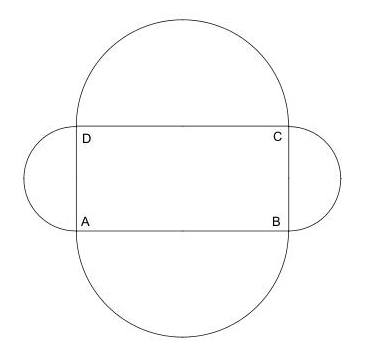
On considère la figure (F) formée d’un rectangle ABCD et de quatre demi-disques extérieurs à ce rectangle et de diamètre respectifs AB, BC, CD et DA. De plus, x = DA. Le périmètre du rectangle est de 20.
1) Préciser entre quelles valeurs doit se trouver x pour que cette figure soit réalisable.
2) Déterminer l’aire de cette figure, notée S(x).
3) Pour quelle valeur de x cette aire est-elle minimale ? Quelle est alors la valeur de cette aire et la nature du rectangle ?
Exercice plus difficile :
On considère un trapèze ABCD tel que les angles A^BC et D^CB aient la même mesure α.
4) Déterminer les valeurs de α pour que le trapèze ABCD ait une aire maximale sachant que les côtés AB, BC et CD mesurent un mètre.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, dérivation, optimisation, surface.
Exercice précédent : Dérivation – Fonctions, huit vrai/faux à justifier – Première

