Maths de première : exercice sur la dérivabilité avec pente de tangente. Calculs, formules, racines, fonctions rationnelles, courbe.
Exercice N°296 :
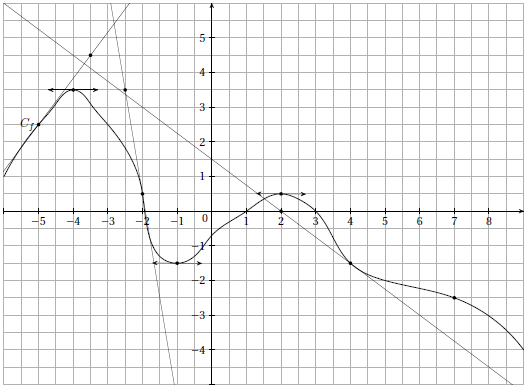
Voici ci-dessus la courbe représentative Cf d’une fonction f définie sur R.
1) D’après le graphique, donner la valeur de f ‘ (−4) en justifiant.
2) Puis f ‘ (−5).
3) Puis f ‘ (−2).
4) Puis f ‘ (4).
5) Déterminer l’équation de la tangente à Cf au point d’abscisse -2.
6) On sait que f ‘ (7) = – 1/3 ; tracer T7, tangente à la courbe Cf au point d’abscisse 7.
7) Résoudre graphiquement f ‘ (x) > 0.
Autre chose :
La fonction c est définie sur R par
c(x) = x2.
8) Avec la définition du nombre dérivé, démontrer que
c ‘ (x) = 2x pour tout réel x .
9-13) Pour chaque fonction ci-dessous, donner son domaine de définition, de dérivabilité, et calculer sa fonction dérivée :
9) g(x) = 2x3 + x − 1/x,
10) h(x) = 3x√x (avec un “x (iks)” à droite du 3 et à gauche de la racine – pas de “fois”),
11) k(x) = (x − 1)/(2x − 3),
12) l(x) = (4x − 1)(x² + 3),
13) m(x) = (1 – x)/(x² + 1).
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, dérivabilité, pente, tangente.
Exercice précédent : Dérivation – Rationnelle, signe, variation, tangente – Première

