Maths : exercice de continuité, dérivation de terminale. Fonction, quotient, tableau de variation, solution unique, valeur approchée.
Exercice N°395 :

Exercice N°395 :
On considère la fonction g :
x → (x2 – 4x + 3)/x2
définie sur ]0 ; +∞[.
1) Montrer que pour tout x > 0,
g ‘ (x) = (2(2x – 3))/x3.
2) Dresser le tableau de variation de g.
3) Montrer que l’équation g(x) = 2 a une solution unique
x0 ∈ [1/2 ; 1].
4) Donner une valeur approchée de x0 à 10-2 près.
Partie indépendante :
On donne ci-dessous le tableau de variation de la fonction f.
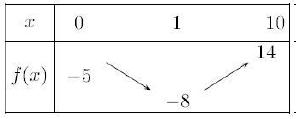
5) Montrer que l’équation f(x) = 0 admet une solution unique notée α sur l’intervalle [0 ; 10].
On donne f(4) = 0.
6) En déduire le signe de f(x) sur [0 ; 10].
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, continuité, dérivation, terminale.
Exercice précédent : Quotients – Fonctions, second degré, courbes, inéquations – Seconde

