Exercice de maths de terminale sur les fonctions avec variations, continuité, équation avec solution unique, coût et quantité, production.
Exercice N°601 :
Exercice N°601 :
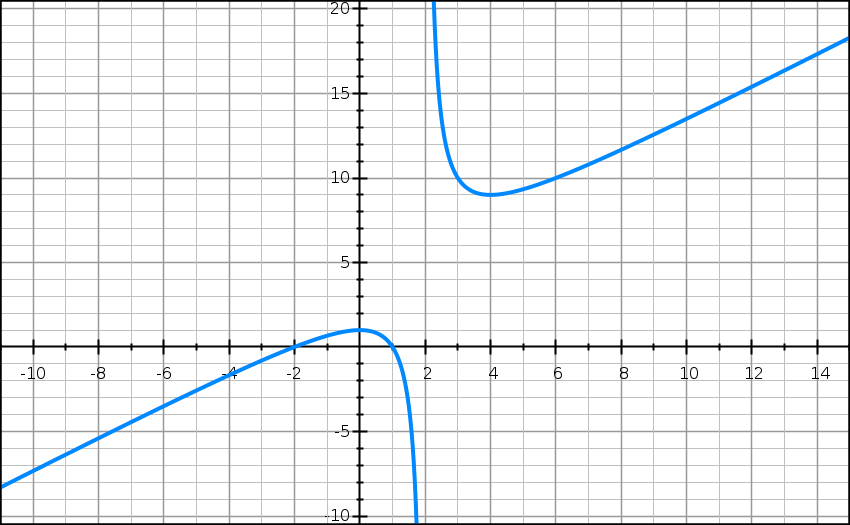
On considère la fonction f définie sur [1 ; 10] par :
f(x) = 2x2 − 30x + 200 + (50/x).
1) Calculer f ‘, la dérivée de f sur [1 ; 10] et montrer que pour tout réel x de cet intervalle :
f ‘ (x) = (4x3 − 30x2 − 50)/(x2) Lis la suite »
Maths : exercice de dérivée, dérivation, terminale, continuité, fonction, variation, racines, rationnelles, puissances, dérivabilité, valeurs.
Exercice N°254 :
Exercice N°254 :
On a la fonction f suivante :
f(x) = {x2 – 2x pour x > 3,
{ x pour x ≤ 3.
1) La fonction est-elle dérivable en 3 ? Lis la suite »
Maths de terminale : exercice de fonctions avec variation et continuité. Signe, tableau de variation, limite, domaine de définition, asymptote.
Exercice N°252 :
Exercice N°252 :
Soit g la fonction définie sur [1 ; +∞[ par
g(x) = 2x3 − 3x2 − 1.
1) Justifier que l’équation g(x) = 0 admet une unique solution α dans l’intervalle [1 ; +∞[. Lis la suite »
Maths de terminale : exercice, fonction, limite, asymptote, rationnelle, tableau de variation, conjecture, intersection, axe, droite.
Exercice N°250 :
On considère la fonction g définie sur ]-∞ ; 2[ ⋃ ]2 ; +∞[
par
g(x) = (x2 + x – 2)/(x – 2)
et Cg sa courbe représentative dans un repère du plan.
1) Conjecturer, à l’aide du graphique, les variations de la fonction g, et les asymptotes à Cg. Lis la suite »
Maths de terminale : exercice de limite avec quotient et asymptote. Calculs avec fonctions rationnelles, racine, soustraction, infini, zéro.
Exercice N°245 :
Exercice N°245 :
1-2-3-4) Calculer les limites suivantes et donner les éventuelles asymptotes des courbes associées aux fonctions.
1) lim x→-∞ ( (3x4 + 2x – 5)/(x4 + 1) ) Lis la suite »
Maths de terminale : exercice de variation de racine carrée. Fonction, tableau de valeurs, croissance, décroissance, domaine de définition.
Exercice N°240 :
Exercice N°240 :
1) Montrer que le domaine de défition de la fonction f définie par
f(x) = √(1 − x²)
est [−1 ; 1].
2) Étudier les variations de la fonction f. Lis la suite »
Exercice de maths de terminale avec équation et inéquation sur cosinus et sinus. Fonctions trigonométriques, formules de cours.
Exercice N°237 :
Exercice N°237 :
1) Résoudre dans [0 ; 2π] l’inéquation
(cos x)2 ≤ 1/2. Lis la suite »
Exercice de maths de terminale de fonction avec polynôme, rationnelle, variation, continuité, équation, dérivées, limites, TVI, courbe.
Exercice N°232 :
Soit g la fonction définie sur R par
g(x) = x3 – 3x – 3.
1) Démontrer que l’équation
g(x) = 0
a une solution unique α dans R. Lis la suite »
Exercice de maths de terminale de fonction avec tan, dérivée, tangente. Trigonométrie, limite, variation, étude de signe, inéquation.
Exercice N°231 :
Soit f la fonction définie sur I = ] –π/2 ; π/2 [ par
f(x) = tan x – x – x3/3.
On appelle g la fonction définie sur I par
g(x) = tan x – x.
1) Montrer que g est impaire. Lis la suite »
Maths de terminale : exercice sur polynôme, racine, inéquation, équation, factorisation. Discriminant, coefficients égaux, second degré.
Exercice N°238 :
Exercice N°238 :
Soit A = √(4 – √7) – √(4 + √7).
1) Calculer A2 et montrer que A2 ∈ N. Lis la suite »
