Maths : exercice d’exponentielle avec algorithme de terminale. Fonction, variation, limite, équation, tangente, position relative, continuité
Exercice N°279 :
On considère la fonction f définie sur R par
f(x) = e−x + x.
On note C sa courbe représentative dans un repère orthonormal.
1) Calculer les limites de f en +∞ et −∞.
Au voisinage de −∞, on pourra démontrer que
f(x) = e−x (1 + xex). Lis la suite »
Maths sur les fonctions avec un polynôme, exercice, convexité, terminale, coût, fixe, marginal, point d’inflexion, lecture graphique.
Exercice N°407 :
Dans une entreprise, le coût total, en euros, pour la fabrication de machines est modélisé par la fonction définie sur l’intervalle [0 ; 100] par l’expression :
C(q)= 0.05q3 – 6q2 + 400q + 1000.
La fonction C est représentée par la courbe ci-dessus dans un repère orthogonal.
1) Quels sont les coûts fixes de production ? Lis la suite »
Exercice de maths de terminale sur les fonctions. Lecture graphique, nombre dérivé, courbe représentative. Tangente, tableau de signe, pente.
Exercice N°405 :
La courbe Cf est la représentation graphique d’une fonction f définie et dérivable sur l’intervalle [0 ; 6].
La courbe Cf est représentée ci-dessous.
Soit A le point du plan de coordonnées (−1 ; 0) et B le point du plan de coordonnées (1 ; 5).
Le maximum de la fonction f est atteint en x = 4/3.
Le point B appartient à la courbe Cf. La droite (AB) est la tangente à la courbe Cf au point B.
1) Par lecture graphique, déterminer les nombres f(1) puis f ‘ (1), où f ‘ est la fonction dérivée de la fonction f sur l’intervalle [0 ; 6] en justifiant la réponse. Lis la suite »
Exercice de maths de terminale de fonction avec courbe, équation réduite, point d’inflexion, tangente, graphique, variation, bénéfice.
Exercice N°404 :
On donne ci-dessus la représentation graphique de la fonction f définie sur [0,5 ; 10] et on note Cf la représentation graphique de la fonction f.
T, T ‘ et T ‘ ‘ sont les tangentes à la courbe au points A d’abscisse 1 et B d’abscisse 4 et C d’abscisse 3/2.
Partie A – En utilisant le graphique :
1) Déterminer f ‘ (1) et donner une valeur approchée aux dixièmes de f ‘ (4). Lis la suite »
Maths de terminale sur les fonctions. Exercice sur un bénéfice, polynôme, rationnelle, droite, coût, quantité, graphique, maximum, dérivée.
Exercice N°403 :
L’entreprise Sheddi produit du tissu en coton. Celui-ci est fabriqué en 1 mètre de large et pour une longueur x exprimée en kilomètre, x étant compris entre 0 et 10.
Le coût total de production en euros de l’entreprise Sheddi est donné en fonction de la longueur x par la formule
C(x) = 15x3 − 120x2 + 500x + 750.
Le graphique ci-dessus donne la représentation graphique de la fonction C.
Les deux parties A et B de cet exercice sont indépendantes.
Partie A : Étude du bénéfice
Si le marché offre un prix p en euros pour un kilomètre de ce tissu, alors la recette de l’entreprise Sheddi pour la vente d’une quantité x est égal à
R(x) = px.
1) Tracer sur le graphique la droite D1 d’équation
y = 400x.
Expliquer, au vu de ce tracé, pourquoi l’entreprise Sheddi ne peut pas réaliser un bénéfice si le prix p du marché est égal à 400 euros. Lis la suite »
Maths de terminale : exercice avec fonction, dérivée et courbe représentative à analyser. Tableau de signe, pente, inéquation et primitive.
Exercice N°402 :
Le plan est muni d’un repère orthonormé (O ; →i ; →j).
La courbe Cf (en traits pleins) représente une fonction f définie et dérivable sur l’intervalle [0 ; 5].
La droite T (en pointillés) est la tangente à Cf au point A(3 ; 1).
La fonction F est définie et dérivable sur [0 ; 5], de dérivée f.
Elle vérifie F(2) = 0.
On note CF sa courbe représentative dans un repère orthonormé.
1) Donner f(1) sans justifier. Lis la suite »
Exercice de maths sur la continuité et solution unique de terminale. Fonctions. Variation, tableau de signe, recette, prix, courbe.
Exercice N°398 :
Exercice N°398 :
Le nombre x ∈ [1 ; 20] désigne un prix en centaine d’euros.
La fonction f représente, en fonction du prix x de l’article, la demande des clients (la quantité d’articles qu’ils sont prêts à acheter à ce prix). Elle est représentée en traits pleins.
La fonction g représente, en fonction du prix x d’un article, l’offre d’un vendeur (la quantité d’articles qu’il est prêt à vendre à ce prix). Elle est tracée en trait pointillés.
1-2-3-4) Par lecture graphique déterminer :
1) Les sens de variation respectifs de f et g sur l’intervalle [1 ; 20]. Lis la suite »
Mots-clés de l’exercice : Maths : exercice de continuité de terminale avec tangente, fonction, variationcourbe représentative, solution unique, tableau de signe, pente.
Exercice N°396 :
On considère une fonction f :
– définie, continue et dérivable sur l’intervalle [−1 ; +∞[,
– strictement croissante sur l’intervalle [0 ; 2],
– strictement décroissante sur les intervalles [- 1 ; 0] et [2 ; +∞[.
On note f ‘ la fonction dérivée de f sur l’intervalle [−1 ; +∞[.
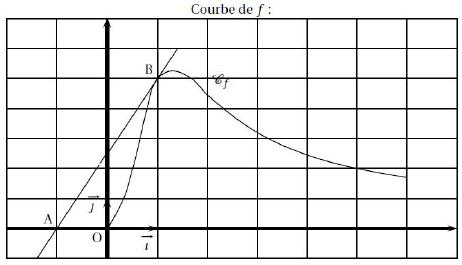
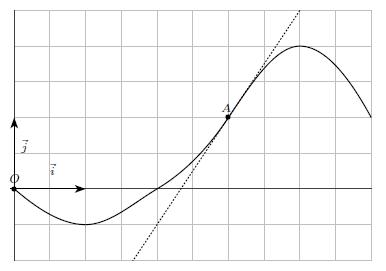
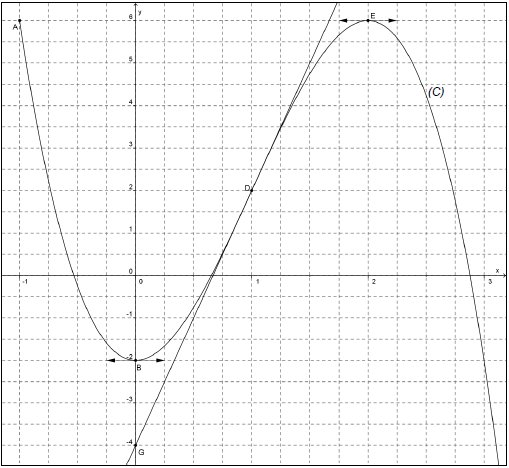
La courbe (C), tracée ci-dessous, représente la fonction f dans le plan muni d’un repère orthogonal.
Elle passe par les points A(−1 ; 6), B(0 ; −2), D(1 ; 2) et E(2 ; 6).
Elle admet au point D une tangente passant par le point G(0 ; −4).
Elle admet au point B et au point E une tangente horizontale.
1) Déterminer f ‘ (1) et f ‘ (2). Justifier les réponses. Lis la suite »
Maths : exercice de continuité, dérivation de terminale. Fonction, quotient, tableau de variation, solution unique, valeur approchée.
Exercice N°395 :
Exercice N°395 :
On considère la fonction g :
x → (x2 – 4x + 3)/x2
définie sur ]0 ; +∞[.
1) Montrer que pour tout x > 0,
g ‘ (x) = (2(2x – 3))/x3. Lis la suite »
Exercice de maths de terminale sur les fonctions avec équation de continuité, dérivée, graphique, fonction, variation, équations, polynôme.
Exercice N°602 :
On a ci-dessus construit la courbe représentative de la fonction h ′, la dérivée d’une fonction h, définie et dérivable sur l’intervalle [−5 ; 3].
1) D’après le graphique, dresser le tableau de signe de h ‘ (x) et le tableau de variation de h sur l’intervalle [−5 ; 3]. Lis la suite »
