Exercice de maths de terminale sur les fonctions avec équation de continuité, dérivée, graphique, fonction, variation, équations, polynôme.
Exercice N°602 :
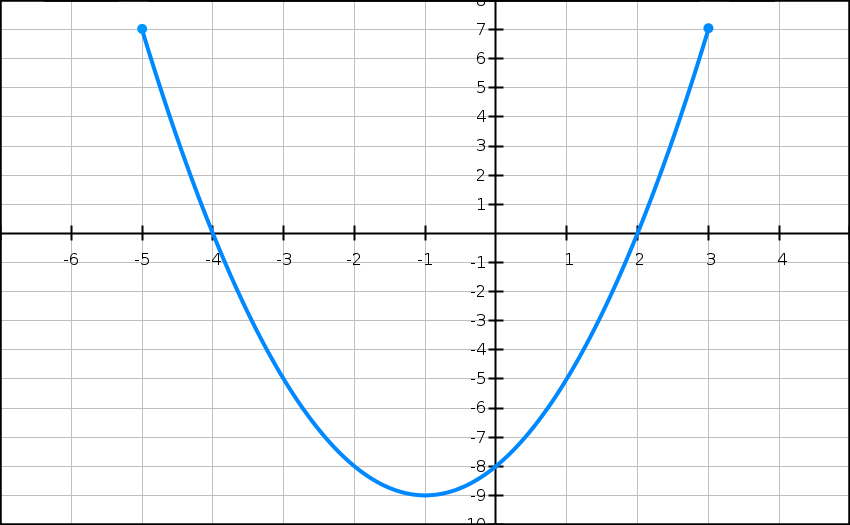
On a ci-dessus construit la courbe représentative de la fonction h ′, la dérivée d’une fonction h, définie et dérivable sur l’intervalle [−5 ; 3].
1) D’après le graphique, dresser le tableau de signe de h ‘ (x) et le tableau de variation de h sur l’intervalle [−5 ; 3].
La fonction h est en fait la fonction :
h :
{ [−5 ; 3] → R,
{ x → h(x) = (x3/3) + x2 − 8x + 1.
2) Déterminer la dérivée de h sur [−5 ; 3] puis étudier son signe sur cet intervalle.
3) En déduire les variations de h sur [−5 ; 3]. On fera clairement figurer les images par h des bornes de l’intervalle d’étude et des racines de h ‘.
4) Vérifiez que ces résultats sont cohérents avec ceux de la question 1).
Approximation de la solution de l’équation h(x) = 5 :
5) Montrer que l’équation h(x) = 5 admet une unique solution α sur l’intervalle [−5 ; 3]. Donner un intervalle comprenant α sur lequel la fonction est monotone.
6) Donner une valeur une valeur approchée de α au centième.
Autre chose :
7) Déterminer le nombre de solutions de l’équation
x3 − 3x2 = −2
sur R et une approximation de ces dernières au centième.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : équation de continuité, dérivée, graphique.
Exercice précédent : Fonctions – Variation, continuité, équation, solution, coût – Terminale

