Maths de première, exercice de dérivée avec fonction rationnelle. Calculs d’image et de nombre dérivé, courbes et tableau de variation.
Exercice N°286 :
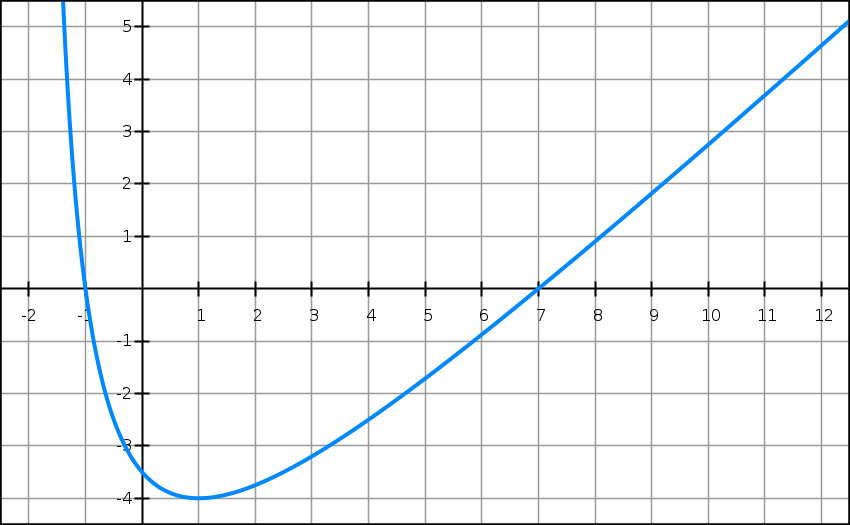
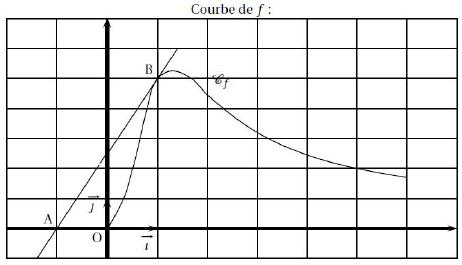
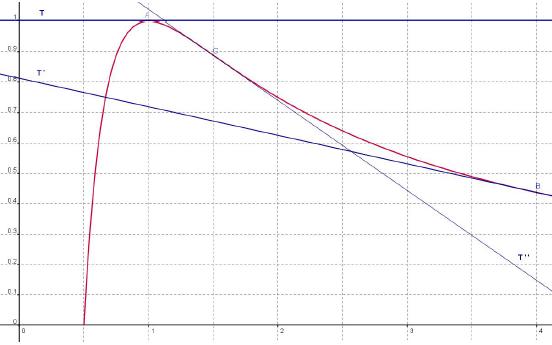
On a tracé ci-dessus, la courbe représentative Cf d’une fonction f définie sur l’intervalle ]−2 ; +∞[. On note f ‘ la dérivée de la fonction f.
1) Par lecture graphique, donner les valeurs de f(1) et de f ‘ (1). Lis la suite »
Exercice de maths de première sur le taux de variation, nombre dérivé, ensemble de dérivabilité, tableau de variations, tangentes.
Exercice N°050 :
Exercice N°050 :
1-2) Des nombres dérivés
Soit f la fonction définie sur R par
f(x) = 1 – x2.
1) Montrer que f est dérivable en a = 2 et calculer f ‘ (2). Lis la suite »
Exercices, dérivées, position relative, maths, terminale, fonction, tableau de signes, position relative, variations, polynôme et racine.
Exercice N°399 :
Exercice N°399 :
Soient f et g les fonctions définies par
f(x) = x2
et
g(x) = x
pour x ∈ R.
On note Pf la parabole représentative de f et D la droite représentative de g dans un repère orthonormé.
1) Dresser le tableau de signes de f(x) − g(x) pour x ∈ R. Lis la suite »
Exercice de maths de terminale sur la limite, l’exponentielle, suite, continuité. Dérivée, tableau de variation, fonction, démonstration.
Exercice N°283 :
Soit n un entier naturel.
On note fn la fonction définie sur l’ensemble R des nombres réels par :
fn(x) = e−nx/(1 + e−x).
On note Cn la courbe représentative de fn dans un repère orthogonal
(O ; →i ; →j).
Les courbes C0, C1, C2 et C3 sont représentées ci-dessus.
1) Démontrer que pour tout entier naturel n, les courbes Cn ont un point A en commun. On précisera ses coordonnées. Lis la suite »
Exercice de maths de terminale avec fonction, dérivée, limite, tableau de variation, suite, somme géométrique, exponentielle, convergence.
Exercice N°282 :
Exercice N°282 :
On considère la fonction f définie sur l’intervalle ]0 ; +∞[ par :
f(x) = x/(ex−1).
On rappelle que la fonction exponentielle est l’unique fonction g dérivable sur R vérifiant :
{ g ‘ (x) = g(x) pour tout x ∈ R et g(0) = 1.
1) Démontrer que limh→0 (eh − 1)/h = 1. Lis la suite »
Maths : exercice d’exponentielle avec algorithme de terminale. Fonction, variation, limite, équation, tangente, position relative, continuité
Exercice N°279 :
On considère la fonction f définie sur R par
f(x) = e−x + x.
On note C sa courbe représentative dans un repère orthonormal.
1) Calculer les limites de f en +∞ et −∞.
Au voisinage de −∞, on pourra démontrer que
f(x) = e−x (1 + xex). Lis la suite »
Maths de terminale: exercice d’exponentielle avec variation, courbe représentative, dérivée, signe, croissance, décroissance, limite.
Exercice N°276 :
Soit f une fonction dérivable sur R dont le tableau de variations est donné ci-contre où a et b désignent deux réels.
1) Déterminer le signe de f ‘ (x) selon les valeurs de x. Lis la suite »
Maths sur les fonctions avec un polynôme, exercice, convexité, terminale, coût, fixe, marginal, point d’inflexion, lecture graphique.
Exercice N°407 :
Dans une entreprise, le coût total, en euros, pour la fabrication de machines est modélisé par la fonction définie sur l’intervalle [0 ; 100] par l’expression :
C(q)= 0.05q3 – 6q2 + 400q + 1000.
La fonction C est représentée par la courbe ci-dessus dans un repère orthogonal.
1) Quels sont les coûts fixes de production ? Lis la suite »
Exercice de maths de terminale sur les fonctions. Lecture graphique, nombre dérivé, courbe représentative. Tangente, tableau de signe, pente.
Exercice N°405 :
La courbe Cf est la représentation graphique d’une fonction f définie et dérivable sur l’intervalle [0 ; 6].
La courbe Cf est représentée ci-dessous.
Soit A le point du plan de coordonnées (−1 ; 0) et B le point du plan de coordonnées (1 ; 5).
Le maximum de la fonction f est atteint en x = 4/3.
Le point B appartient à la courbe Cf. La droite (AB) est la tangente à la courbe Cf au point B.
1) Par lecture graphique, déterminer les nombres f(1) puis f ‘ (1), où f ‘ est la fonction dérivée de la fonction f sur l’intervalle [0 ; 6] en justifiant la réponse. Lis la suite »
Exercice de maths de terminale de fonction avec courbe, équation réduite, point d’inflexion, tangente, graphique, variation, bénéfice.
Exercice N°404 :
On donne ci-dessus la représentation graphique de la fonction f définie sur [0,5 ; 10] et on note Cf la représentation graphique de la fonction f.
T, T ‘ et T ‘ ‘ sont les tangentes à la courbe au points A d’abscisse 1 et B d’abscisse 4 et C d’abscisse 3/2.
Partie A – En utilisant le graphique :
1) Déterminer f ‘ (1) et donner une valeur approchée aux dixièmes de f ‘ (4). Lis la suite »
