Exercice de maths de première sur fonctions affine et second degré. Polynôme, droite, variation, équation, repère, courbe représentative.

Exercice N°058 :

Second degré, affine, polynôme, droite, variation, équation

Exercice N°058 :

Pour les vacances, Marie et Pierre, deux frère et sœur, ont acheté des jouets. Pierre un bonhomme suspendu à un parachute et Marie un arc avec des flèches. Pierre lance son parachute du haut d’une falaise. Au même moment, Marie lance un flèche verticalement du pied de la même falaise.

La hauteur du parachute à l’instant t (en seconde) durant la descente est donnée par la fonction h définie par
h(t) = -5t + 5.2.

La hauteur de la flèche à l’instant t est donnée par la fonction f définie par
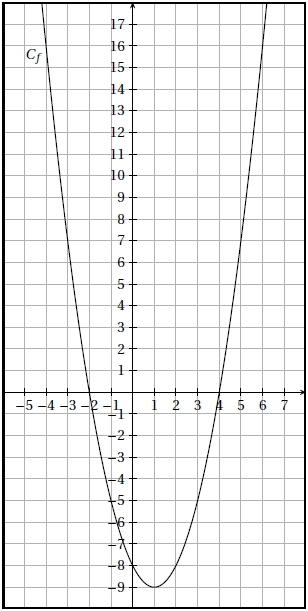
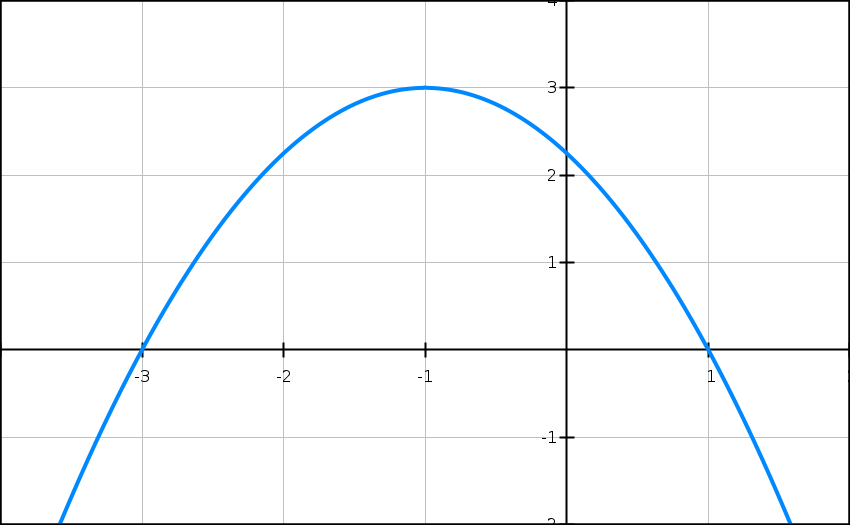
f(t) = -5t2 + 10t.

1) Étudier les variations de f sur R. Lis la suite »

Ecris le premier commentaire

Maths de seconde : exercice de fonctions avec position relative. Parabole, droite, polynôme, affine, tableau de variation, antécédent, égalité.

Exercice N°157 :

Exercice, fonctions, position relative, seconde

On donne f et g définies sur R par
f(x) = x2 − 2x − 8
et
g(x) = − 3x − 2.

1) Quelle est la nature de f et g ? Représenter Cg. Lis la suite »

Ecris le premier commentaire

Maths de première sur le second degré : exercice pour résoudre une inéquation quotient. Tableau de signe, domaine de définition.

Exercice N°651 :

Exercice, résoudre une inéquation quotient, second degré, domaine de définition, première

Exercice N°651 :

1) Résoudre l’inéquation
(-x2 + 4)/(3x2 + 2x – 1) ≤ 0. Lis la suite »

Ecris le premier commentaire

Maths de seconde sur le second degré : exercice sur forme canonique et factorisation. Minimum, fonction, tableau de variation.

Exercice N°156 :

Exercice, forme canonique, factorisation, second degré, symétrie, fonction, tableau de variation, première

Exercice N°156 :

Soit f définie pour tout x ∈ R par
f(x) = x2 − 3x + 2.
La courbe représentative de f s’appelle Cf.

1) Donner l’équation de l’axe de symétrie de la parabole Cf. Lis la suite »

Ecris le premier commentaire

Maths : exercice d’encadrement de carré en seconde. Fonction, inégalités, implications, images et antécédents, variation, conséquence.

Exercice N°650 :

Carré, implications, images, antécédents, seconde

Exercice N°650 :

1-3) Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse et fournir un contre-exemple lorsqu’elle est fausse.

1) x2 ≥ 3 ⇒ x > 1, Lis la suite »

Ecris le premier commentaire

Maths de terminale : second degré, dérivée, équation. Lecture graphique, courbe, tableau de variation, droite, dérivée, inéquation, polynôme.

Exercice N°400 :

Second degré, dérivée, équation, graphique, polynôme, terminale

Exercice N°400 :

On a représenté la courbe C d’une fonction f définie sur [−3,5 ; 1,5]. Répondre aux questions suivantes par lecture graphique : Lis la suite »

Ecris le premier commentaire

Maths de terminale, exercice de dérivée : cosinus, racine, exponentielle, fraction rationnelle. Dérivabilité et calculs avec les formules.

Exercice N°242 :

Dérivées, cosinus, racine, puissance, fraction, produit

Exercice N°242 :

1-5) Pour chacune des fonctions suivantes, justifier qu’elle est dérivable, trouver son domaine de dérivabilité, puis calculer sa dérivée.

1) f(x) = cos(2x + π/4), Lis la suite »

Ecris le premier commentaire

Maths de première sur les fonctions polynômes du second degré. Coûts, recette, exercice pour calculer le bénéfice maximal, parabole, sommet.

Exercice N°260 :

coût, exercice, calculer bénéfice maximal, recette, second degré, première

Exercice N°260 :

Dans une entreprise, les coûts de fabrication de q objets sont donnés, en euros, par :
C(q) = 0,1q2 + 10q + 1500,
pour q appartient à [0 ; 500].

L’entreprise vend chaque objet fabriqué 87 €.

1) Quels sont les coûts fixes ? Lis la suite »

Ecris le premier commentaire

Maths de première : exercice de dérivée et variation avec tangente. Fonction rationnelle, équation de droite, racine, courbe représentative.

Exercice N°289 :

Exercice, dérivée, variation tangente, fonction rationnelle, première

Soit f la fonction définie sur R par
f(x) = (x2 − 4x + 7)/(x2 + 3).
On note Cf sa courbe représentative dans le plan muni d’un repère.

1) Montrer que la dérivée de la fonction f est la fonction f ‘ définie sur R par Lis la suite »

Ecris le premier commentaire

Exercice de maths de première sur la dérivation, fonction, courbes, nombres dérivés. Tangente parallèle, axe abscisses, intersection.

Exercice N°288 :

Dérivation, fonction, tangente parallèle, axe abscisses, première

Soit f une fonction définie et dérivable sur R. On note f ‘ la dérivée de la fonction f.
On donne ci-dessus la courbe Cf représentant la fonction f.
La courbe Cf coupe l’axe des abscisses au point A(−2 ; 0) et lui est tangente au point B d’abscisse 6.
La tangente à la courbe au point A passe par le point M(−3 ; 3).
La courbe Cf admet une deuxième tangente parallèle à l’axe des abscisses au point C d’abscisse 0.

À partir du graphique et des données de l’énoncé, répondre aux questions suivantes.

1) Dresser sans justification le tableau de variations de la fonction f sur R. Lis la suite »

Ecris le premier commentaire

« Articles précédents     Articles suivants »
✕
FrenchMaths.com

GRATUIT
VOIR