Maths de première : exercice de dérivée et variation avec tangente. Fonction rationnelle, équation de droite, racine, courbe représentative.
Exercice N°289 :
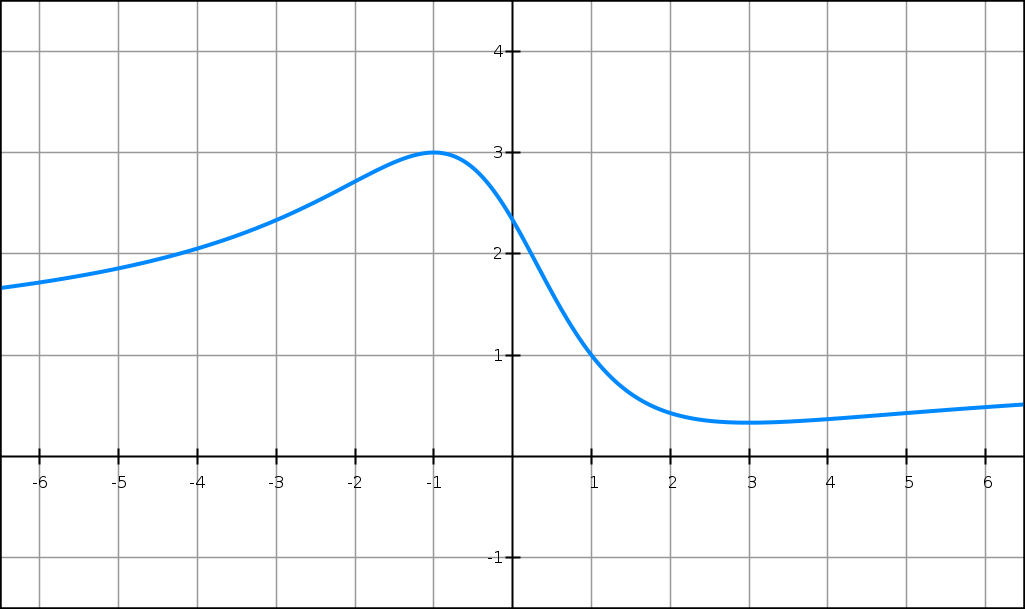
Soit f la fonction définie sur R par
f(x) = (x2 − 4x + 7)/(x2 + 3).
On note Cf sa courbe représentative dans le plan muni d’un repère.
1) Montrer que la dérivée de la fonction f est la fonction f ‘ définie sur R par
f ‘ (x) = 4(x2 − 2x – 3)/(x2 + 3)2 .
2) Étudier les variations de la fonction f.
3) Donner une équation de la tangente T à la courbe Cf au point d’abscisse 1.
Représenter la tangente T sur le graphique ci-dessus.
4) Donner le sens de variation de la fonction
l(x) = √(3x + 2)
sur I = ]-2/3 ; +∞[.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, dérivée, variation, tangente.
Exercice précédent : Dérivation – Fonction, nombre dérivé, courbe, tangente – Première

