Exercice de maths de première sur la dérivation, fonction, courbes, nombres dérivés. Tangente parallèle, axe abscisses, intersection.
Exercice N°288 :

Soit f une fonction définie et dérivable sur R. On note f ‘ la dérivée de la fonction f.
On donne ci-dessus la courbe Cf représentant la fonction f.
La courbe Cf coupe l’axe des abscisses au point A(−2 ; 0) et lui est tangente au point B d’abscisse 6.
La tangente à la courbe au point A passe par le point M(−3 ; 3).
La courbe Cf admet une deuxième tangente parallèle à l’axe des abscisses au point C d’abscisse 0.
À partir du graphique et des données de l’énoncé, répondre aux questions suivantes.
1) Dresser sans justification le tableau de variations de la fonction f sur R.
2) Déterminer f ‘ (0) en justifiant.
3) Déterminer les solutions de l’équation f ‘ (x) = 0 en justifiant.
4) Déterminer une équation de la tangente à la courbe Cf au point A. En déduire la valeur de f ‘ (−2). Justifier les réponses.
5) On donne f ‘ (2) = 3/4.
Calculer les coordonnées du point d’intersection de la tangente à la courbe Cf au point D avec l’axe des abscisses.
6) Une des trois courbes ci-dessous est la représentation graphique de la fonction f ‘. Déterminer laquelle.
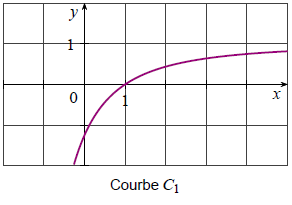
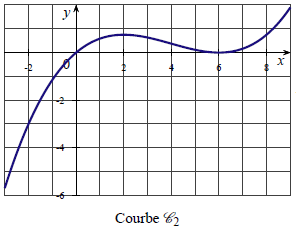

Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : tangente, parallèle, axe, abscisses.
Exercice précédent : Dérivation – Calculs, formules, racine, rationnelle – Première

