Maths : exercice d’étude de fonction de seconde. Images, antécédent, résolution graphique d’équation et d’inéquation, tableau de variation.
Exercice N°095 :
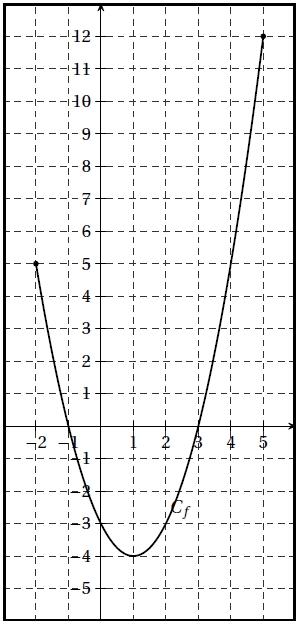
1) Déterminer le domaine de définition Df. Lis la suite »
Maths : exercice d’étude de fonction de seconde. Images, antécédent, résolution graphique d’équation et d’inéquation, tableau de variation.
Exercice N°095 :

1) Déterminer le domaine de définition Df. Lis la suite »
Exercice de maths de seconde sur les fonctions avec équations, inéquations sur graphique. Domaine de définition, images, antécédents, courbe.
Exercice N°094 :
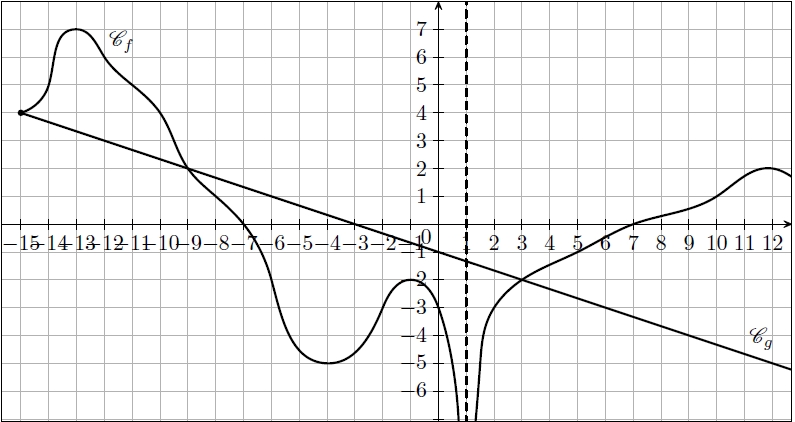
Répondre aux questions suivantes en utilisant le graphique.
1) Déterminer l’ensemble de définition de f et g. Lis la suite »
Exercice de maths de seconde sur les fonctions affines et leur sens de variation. Droite, coefficients directeur, calculs, pente.
Exercice N°080 :

Exercice N°080 :
1-2-3-4-5) Dans chaque cas, donner le sens de variation et faire un tableau de signe de la fonction proposée :
1) f(x) = 2x – 3, Lis la suite »
Maths : exercice d’exponentielle avec fonction et suite. Courbes représentatives, variatios, tangente, abscisse, ordonnée, terminale.
Exercice N°277 :
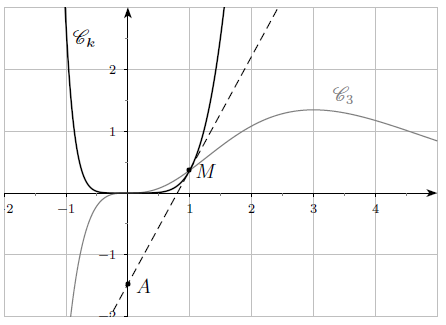
Pour tout entier n ≥ 1, on note fn la fonction définie sur R par
fn(x) = xne-x.
Cn est la courbe représentative de fn dans un repère orthonormé.
Sur la figure ci-dessous, on a tracé la courbe C3 ainsi qu’une courbe Ck pour un certain k ∈ N* tel que la tangente Tk à Ck au point M d’abscisse 1 coupe l’axe des ordonnées en A de coordonnées (0 ; –4/e).
On cherche à déterminer la valeur de k :
1) Étudier les variations de f1 et dresser son tableau de variations. Lis la suite »
Maths de terminale : exercice de primitive, d’intégrale et de convexité, exponentielle, tangente, position relative, courbe, aire, variation.
Exercice N°476 :
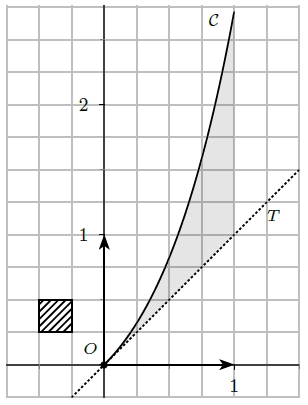
Le plan est muni d’un repère orthonormé (O ; →i ; →j) d’unité graphique 2 cm.
Soit f la fonction définie sur l’intervalle [0 ; 1] par
f(x) = xex.
On note F la primitive de f qui s’annule en x = 1.
On note C la courbe représentative de la fonction f.
Soit b une constante réelle et g la fonction définie sur [0 ; 1] par
g(x) = (x + b)ex.
On répondra par des considérations graphiques pour les quatre premières seulement.
1) Exprimer, en unités d’aires, l’aire du carré hachuré. Lis la suite »
Maths : exercice de primitive et aire de terminale. Lecture graphique, fonction, dérivée, pente, tangente, surface sous la courbe, signe.
Exercice N°475 :
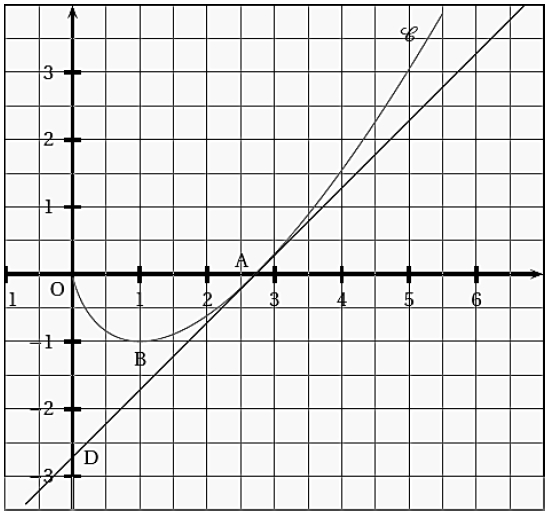
La courbe C ci-dessus représente, dans un repère orthonormé, une fonction f définie et dérivable sur ]0 ; +∞[.
On note f ‘ la fonction dérivée de f. La courbe C passe par les points A(e ; 0) et B(1 ; −1).
La courbe C admet une tangente parallèle à l’axe des abscisses au point d’abscisse 1 et la tangente au point d’abscisse e passe par le point D(0 ; −e).
1) Déterminer une équation de la droite (AD). Lis la suite »
Exercice de maths de terminale sur les primitives, fonction exponentielle, dérivée, intégrale, convexité, point d’inflexion, courbe, TVI.
Exercice N°474 :
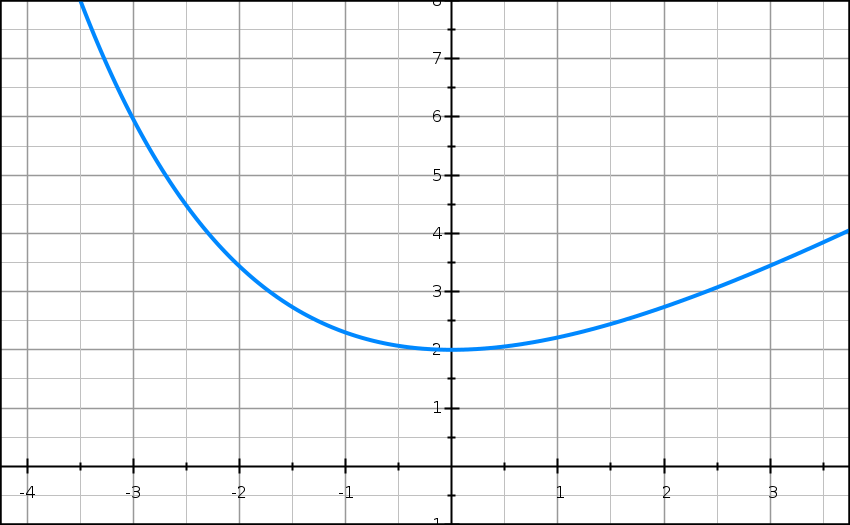
On considère la fonction f définie sur R par
f(x) = 2e−0,5x + x.
On note f la courbe représentative de la fonction f dans le plan muni d’un repère orthogonal (unités graphiques : 2 cm sur l’axe des abscisses et 1 cm sur l’axe des ordonnées).
1) Calculer f ‘ (x). Lis la suite »
Maths de terminale : exercice de logarithme népérien avec suite, algorithme. Variation de fonction, construction de termes.
Exercice N°355 :
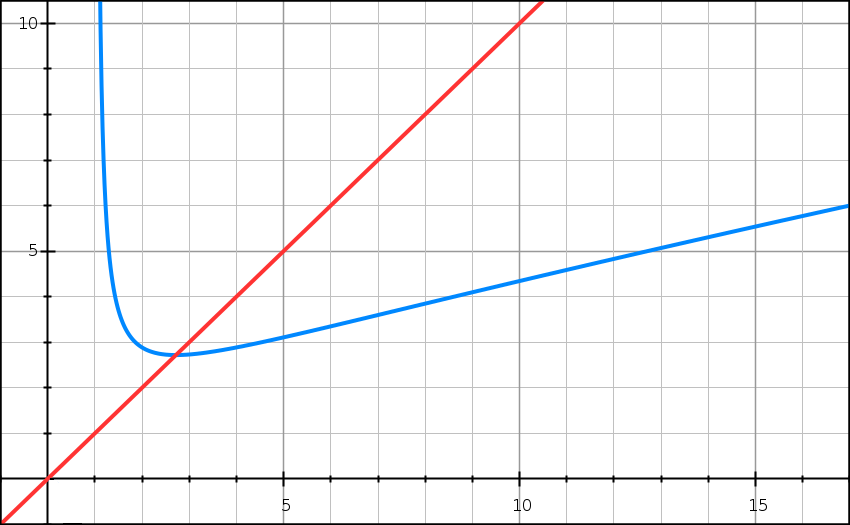
On considère la fonction f définie sur l’intervalle ]1 ; +∞[ par
f(x) = x/(ln x).
Ci-dessus, on a tracé dans un repère orthogonal la courbe C représentative de la fonction f ainsi que la droite D d’équation y = x.
1) Calculer les limites de la fonction f en +∞ et en 1. Lis la suite »
Exercice corrigé sur courbe de Lorenz. Maths de terminale sur les primitives et intégrales avec aire, fonctions affine et polynôme.
Exercice N°473 :
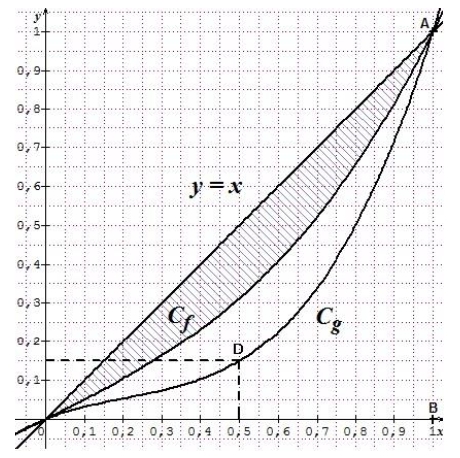
Les deux courbes Cf et Cg représentées ci-dessus illustrent la répartition des richesses dans deux pays 1 et 2. Elles sont définies sur [0 ; 1] et s’appellent
des courbes de Lorentz.
En abscisses, x représente le pourcentage de personnes les plus pauvres par
rapport à la population totale et en ordonnées, y représente le pourcentage de
richesses du pays que ces personnes possèdent.
1) Interpréter économiquement pour le pays 2 les coordonnées du point D de g. Lis la suite »
Exercice de maths de terminale sur primitive et intégrale, fonction rationnelle, étude de signe, aire sous la courbe, bénéfice, moyenne.
Exercice N°471 :
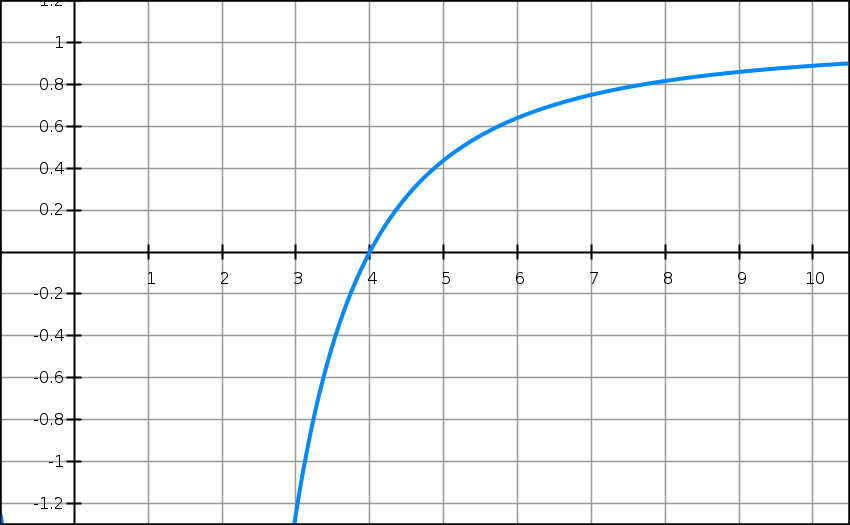
On considère la fonction définie sur [3 ; 10] par
f(x) = (x2 – 2x – 8)/(x – 1)2.
On donne ci-dessus sa courbe Cf dans un repère orthogonal d’unités graphiques : 2 cm en abscisses et 5 cm en ordonnées.
1) Déterminer par calcul le signe de f(x) sur [3 ; 10]. Lis la suite »