Maths : exercice d’exponentielle avec fonction et suite. Courbes représentatives, variatios, tangente, abscisse, ordonnée, terminale.
Exercice N°277 :
Pour tout entier n ≥ 1, on note fn la fonction définie sur R par
fn(x) = xne-x.
Cn est la courbe représentative de fn dans un repère orthonormé.
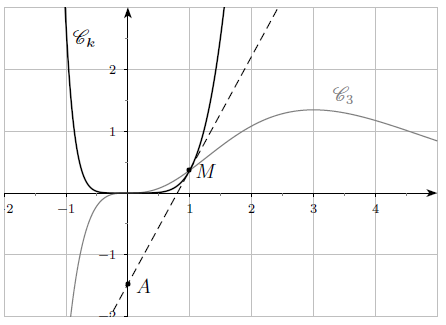
Sur la figure ci-dessous, on a tracé la courbe C3 ainsi qu’une courbe Ck pour un certain k ∈ N* tel que la tangente Tk à Ck au point M d’abscisse 1 coupe l’axe des ordonnées en A de coordonnées (0 ; –4/e).
On cherche à déterminer la valeur de k :
1) Étudier les variations de f1 et dresser son tableau de variations.
2) A l’aide de la représentation graphique, justifier que k ≠ 1.
3) Démontrer que pour tout entier n ≥ 1, toutes les courbes Cn passent par deux points fixes dont on donnera les coordonnées.
4) Vérifier que pour tout entier n ≥ 2 et tout nombre x,
fn ‘ (x) = xn – 1(n – x)e-x.
5) Sur la figure, f3 semble admettre un maximum pour x = 3. Démontrer cette conjecture.
6) Démontrer que la tangente Tk en M à la courbe Ck coupe l’axe des ordonnées au point de coordonnées (0 ; (2 – k)/e).
7) En déduire la valeur de k.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, exponentielle, fonction, suite.
Exercice précédent : Exponentielle – Fonction, dérivée, courbe, variations – Terminale

