Exercice de maths de terminale sur le logarithme népérien avec limites, équations, inéquations, fonction, second degré, tangente.
Exercice N°352 :
Exercice N°352 :
1-2-3-4) Étudier les limites aux bornes de l’intervalle I :
1) f1(x) = (ln x)4 avec I = R+*. Lis la suite »
Exercice de maths de terminale sur le logarithme népérien, suite, algorithme. Fonction, dérivée, variations, TVI, limite, récurrence.
Exercice N°350 :
Exercice N°350 :
Étude d’une fonction :
On considère la fonction f définie et dérivable sur l’intervalle
[0 ; +∞[par
f(x) = 5 ln(x + 3) − x.
On appelle f ‘ la fonction dérivée de la fonction f sur [0 ; +∞[.
1) Calculer f ‘ (x) et étudier son signe sur [0 ; +∞[. Lis la suite »
Maths de terminale : exercice de logarithme népérien avec bénéfice, quotient, dérivée, variation, économie, maximum, unitaire, total.
Exercice N°423 :
Exercice N°423 :
Une entreprise de sous–traitance fabrique des pièces pour l’industrie automobile. Sa production pour ce type de pièces varie de 1000 à 5000 pièces par semaine, selon la demande. On suppose que toutes les pièces produites sont vendues.
Le bénéfice unitaire, en euro, en fonction du nombre de pièces produites par semaine, est modélisé par la fonction f définie sur [1 ; 5] par :
f(x) = ( 2ln(x) + 1 )/x,
avec x exprimé en millier de pièces et f(x) exprimé en euro.
1) Montrer que, sur [1 ; 5],
f ‘ (x) = ( 1 – 2ln(x) )/x2. Lis la suite »
Maths de terminale : exercice sur le logarithme népérien avec tangente, position relative, dérivée, graphique, droite et courbe.
Exercice N°422 :
Les fonctions g et h sont définies sur ]0 ; + ∞[ par
g(x) = ln(x)/(x2)
et
h(x) = ln(x).
La courbe Cg a été tracée ci-dessus.
1) Étudier la position de la courbe Cg par rapport à la courbe Ch. Lis la suite »
Maths : exercice sur le logarithme népérien, terminale, application économique. Dérivée, variation, signe, bénéfice, solution unique, minimum.
Exercice N°420 :
Exercice N°420 :
Une entreprise fabrique et vend à des particuliers des panneaux solaires photovoltaïques produisant de l’électricité.
Elle en produit chaque mois entre 50 et 2500.
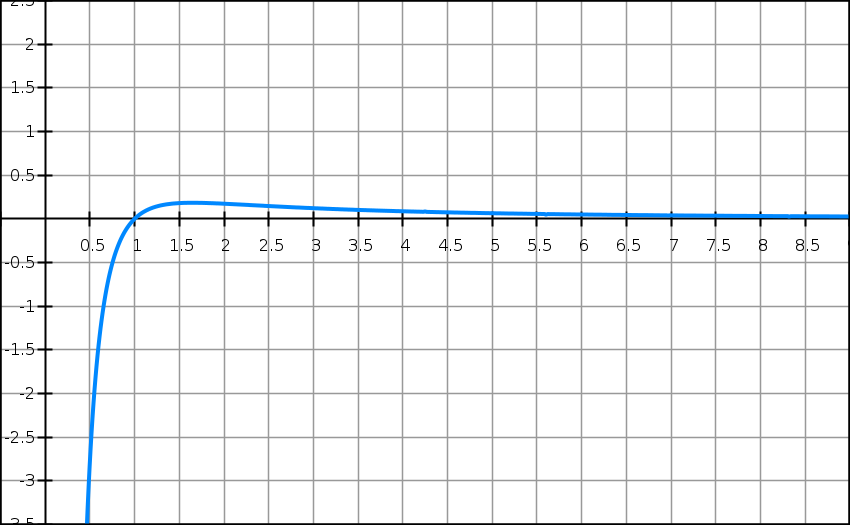
Soit f la fonction définie sur l’intervalle [0,5 ; 25] par
f(x) = 18ln(x) − x2 + 16x − 15.
Si x représente le nombre de centaines de panneaux solaires fabriqués et vendus, alors on admet que f(x) représente le bénéfice mensuel de l’entreprise, en milliers d’euros.
On suppose que f est dérivable sur [0,5 ; 25], et on note f ‘ sa fonction dérivée.
1) Calculer f ‘ (x). Lis la suite »
Maths de terminale : exercice sur le logarithme népérien avec équation, inéquation, calculs, domaine de définition, intervalle, fonction.
Exercice N°419 :
Exercice N°419 :
1) Calculer ln(e3) − 3ln(1), Lis la suite »
Exercice de maths de terminale de logarithme népérien, équation, inéquation, solution unique, convexité, position relative, tangente.
Exercice N°416 :
1) Résoudre l’équation suivante dans R :
ln (x2 – 2x – 3) = ln x. Lis la suite »
Exercice de maths de terminale sur la primitive, exponentielle, suite, intégrale, variation, algorithme, convergence, limite, dérivation.
Exercice N°459 :
Exercice N°459 :
On considère la suite (In) définie pour n entier naturel non nul par :
In = ∫[de 0 à 1] xnex2dx.
Soit g la fonction définie par
g(x) = xex2.
1) Démontrer que la fonction G définie sur R par
G(x) = (1/2)ex2
est une primitive sur R de la fonction g. Lis la suite »
Exercice de terminale avec logarithme népérien, exponentielle, convexité, intégrale, aire, courbe, pourcentage, point d’inflexion, inéquation.
Exercice N°418 :
Exercice N°418 :
1-2-3-4-5-6) Questionnaire à choix unique :
1) Le réel ln(e2) − e + 2ln(1) est égal à :
a) 2 – e,
b) e2 – e,
c) 0. Lis la suite »
Maths de terminale : exercice de logarithme népérien, primitive, intégrale. Tableau, signe, variation, continuité, dérivée, aire sous courbe.
Exercice N°417 :
Exercice N°417 :
On considère la fonction f définie sur ]0 ; 6] par
f(x) = x(ln x – 1).
1) Montrer que, pour tout x de ]0 ; 6], on a :
f ′ (x) = ln x. Lis la suite »
