frenchmaths.com (par Sylvain Jeuland)

Exercice de terminale avec logarithme népérien, exponentielle, convexité, intégrale, aire, courbe, pourcentage, point d’inflexion, inéquation.

Exercice N°418 :

Exercice N°418 :

1-2-3-4-5-6) Questionnaire à choix unique :

1) Le réel ln(e²) − e + 2ln(1) est égal à :
a) 2 – e,
b) e² – e,
c) 0.

g est la fonction définie sur [0 ; 10] par
g(x) = 100xe^−x + 1.
2) C_g admet un point d’inflexion de coordonnées :
a) (2 ; 200e⁻² + 1),
b) (−2 ; 200e² + 1),
c) (100 ; 200).

3) L’ensemble de solution de l’inéquation ln(3 − x) < 1 est :
a) ]3 − e ; +∞[,
b) ]3 − e ; 3[,
c) ]2 ; 3[.

Une entreprise a un chiffre d’affaire de 200 000 d’euros en 2028 et de 292820 euros en 2032.
4) Le pourcentage moyen annuel d’augmentation du chiffre d’affaire entre 2028 et 2032 est :
a) 36,6 %,
b) 11,6 %,
c) 10 %.

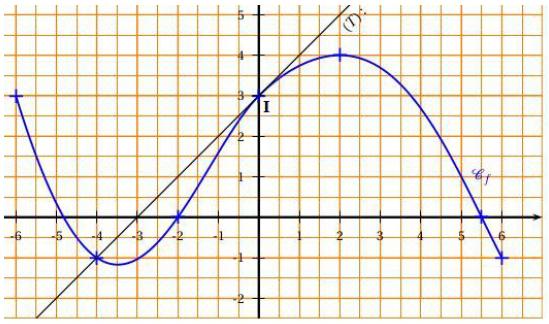
Pour les deux questions suivantes, on considère la courbe C_f représentative d’une fonction f définie et dérivable sur l’intervalle [−6 ; 6].
La droite (T) est tangente à la courbe C_f au point I de coordonnées (0 ; 3).

5) Le nombre dérivé de f en 0 est :
a) 0,
b) 1,
c) 3.

6) On pose J = ∫₀² f(x)dx.
a) 26 < J < 32,
b) 5 < J < 6,
c) 6 < J < 8.

Bon courage,
Sylvain Jeuland

Mots-clés de l’exercice : logarithme, exponentielle, convexité, intégrale.

Exercice précédent : Logarithme Népérien – Tableaux, solution unique, primitive – Terminale