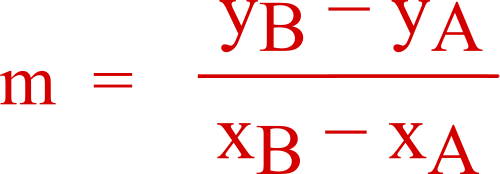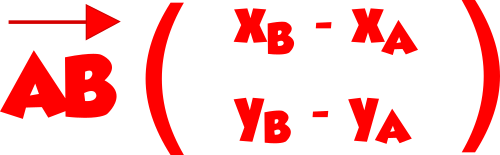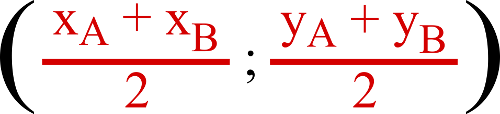frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

*) Déterminer pour cette série :

1) la moyenne :

La formule de la moyenne est :

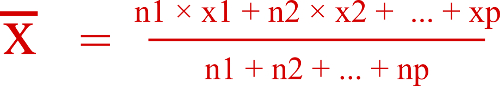
Ici ^–x = ^{(29×0 + 32×1 + 26×2 + 6×3 + 23×4 + 8×6 + 1×8)}/_{(29 + 32 + 26 + 6 + 23 + 8 + 1)}
= ²⁵⁰/₁₂₅ = 2.

La moyenne de cette série est 2.

2) la médiane :

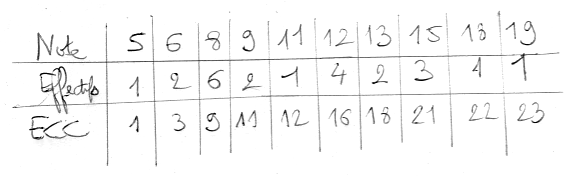
Pour obtenir la médiane, on regarde si l’effectif total est pair ou impaire. Ici N=125, donc on va considérer l’unique valeur centrale qui est la 125/2 = 62,5 donc la 63ème (62 valeurs à gauche et 62 valeurs à droite).

Ensuite, pour tout calcul de médiane (ou quartile), il faut faire le tableau des Effectifs Cumulés Croissants (ECC) pour situer dans quelle case sera la 63ème valeur.

Comme il n’y a que 61 éléments en dessous de la valeur 1 et on arrive à 87 éléments pour la valeur 2, on constate que la 63ème valeur est 2.

Donc la médiane Me = 2 pour cet effectif total impair.

3) le premier et le troisième quartile :

Pour calculer Q1, il faut prendre la valeur numéro 0,25 × N, N étant l’effectif total.
0,25 × 125 = 31,25. On prend la suivante (la 32ème) car comme on veut qu’au moins 25% des valeurs soient en dessous de Q1, si on prend la 31ème, on n’aura pas les 25%. Donc la 32ème.

D’après le tableau des ECC, la 32ème valeur se trouve dans la case en dessous de la valeur 1, car pour 0 on est seulement à un ECC de 29, et on va jusqu’à 61 pour 1.

Donc Q1 = 1.

Pour calculer Q3, il faut prendre la valeur numéro 0,75 × N, N étant l’effectif total.
0,75 × 125 = 93,75. On prend la suivante (la 94ème) car comme on veut qu’au moins 75% des valeurs soient en dessous de Q1, si on prend la 93ème, on n’aura pas les 75%. Donc la 94ème.

D’après le tableau des ECC, la 94ème valeur se trouve dans la case en dessous de la valeur 4, car pour 3 on est seulement à un ECC de 93, et on va jusqu’à 116 pour 14.

Donc Q3 = 4.

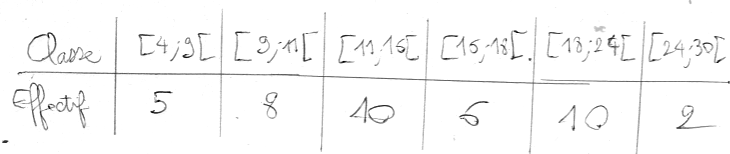
4) Compléter la ligne des fréquences ci-dessus. Détailler les calculs :

Pour calculer une fréquence, on utilise la formule suivante :

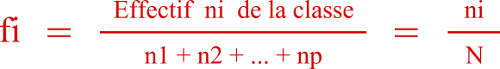
15/125 = 0,12 ; 36/125 = 0,288 ; 40/125 = 0,40 ; 22/125 = 0,176 ; 6/125 = 0,048 deux fois.

5) Calculer le trajet moyen. Détailler le calcul :

On prend les valeurs du milieu des intervalles pour faire le calcul du trajet moyen ^–t soient 7.5, 12.5, 22.5, 37.5, 52.5, 75.

Ici ^–t = ^{(15×7.5 + 36×12.5 + 40×22.5 + 22×37.5 + 6×52.5 + 6×75)}/_{(15 + 36 + 40 + 22 + 6 + 6)}
= ^3052.5/₁₂₅ = 24,42.

6) Quel est le pourcentage d’élève de seconde de ce lycée qui ont au moins 30 minutes de trajet pour venir au lycée. Justifier la réponse :

On compte les effectifs qui mettent plus de 30 minutes à venir : 22 + 6 + 6 = 34.
Puis on fait le tableau du pourcentage avec la proportionnalité et le produit en croix.

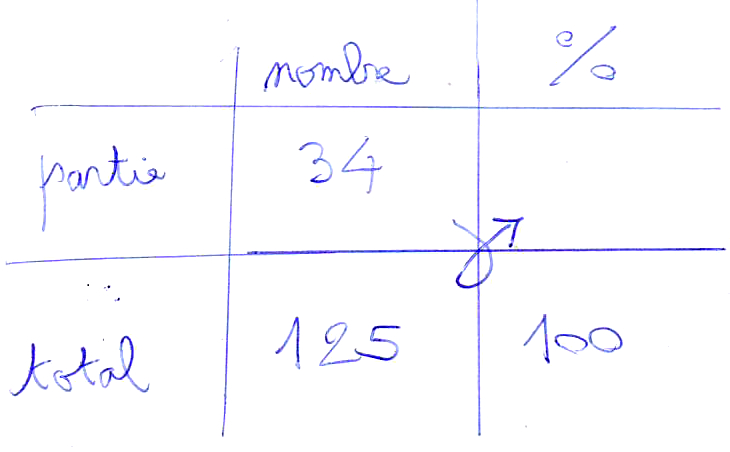
p = 34×100/125 = 27,2%. Le pourcentage d’élèves qui ont au mooins 30 minutes de trajet est de 27,2%.

7) Quel est le temps moyen passé devant l’ordinateur par les filles interrogées ?

L’astuce est de calculer le temps total des élèves, soit 125×64 = 8000 minutes.
Puis le temps total des garçons, soit 75×72 = 5400 minutes.
Le temps total des filles est donc de 8000 – 5400 = 2600 minutes pour 125-75 = 50 filles.

Leur temps moyen est donc de 2600/50 = 52 minutes.

Bonne compréhension,
Sylvain

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Montrer que M ∈ C ⇔ MI² = 25.

Ici, on a du ^→MA et du ^→MB, cela fait deux vecteurs différents et il serait mieux d’avoir un seul vecteur avec le point M.
Du coup, l’astuce habituelle est de prendre le point I le milieu de [AB]et de le mettre au milieu des vecteurs précités avec la relation de Chasles.

^→MA.^→MB = 16
⇔ (^→MI + ^→IA).(^→MI + ^→IB) = 16

L’idée est de développer avec la double distributivité qui marche avec les « . » comme les « × ».

⇔ ^→MI.^→MI + ^→MI.^→IB + ^→IA.^→MI + ^→IA.^→IB = 16

Quand on fait le produit scalaire de deux fois le même vecteur, cela donne la distance au carré, on enlève les flèches.

⇔ MI² + ^→MI.^→IB + ^→IA.^→MI + ^→IA.^→IB = 16

On peut inverser les vecteurs dans un produit scalaire pour avoir les ^→MI devant.

⇔ MI² + ^→MI.^→IB + ^→MI.^→IA + ^→IA.^→IB = 16

Là, il faut factoriser par ^→MI devant ^→IB et ^→IA.

⇔ MI² + ^→MI.(^→IB + ^→IA) + ^→IA.^→IB = 16

Comme I est le milieu de [AB], on a donc ^→IB + ^→IA = ^→0. On peut donc enlever le ^→MI.^→0 car cela donne 0.

⇔ MI² + ^→IA.^→IB = 16

Les vecteurs ^→IA et ^→IB sont diamétralement opposés donc quand on fait le produit scalaire, cela donne IA × IB × (-1)
= AB/2 × AB/2 × (-1) (car IA et IB valent la moitié de AB).
= 6/2 × 6/2 × (-1)
= -9.

On obtient donc :

⇔ MI² – 9 = 16
⇔ MI² = 25

2) Déterminer alors précisément l’ensemble C :

On a donc MI = 5 car on est en géométrie donc on reste dans les nombre positifs.
Du coup, M est a distance de 5 du point I.

L’ensemble C des points vérifiant ^→MA.^→MB = 16 est le cercle de centre I milieu de [AB] et de rayon 5.

3) En utilisant les coordonnées des vecteurs, déterminer précisément l’ensemble D des points M du plan tels que ^→AM.^→BC = 3 :

A(-1 ; 2), B(2 ; -2), C(-2 ; -1) d’après l’énoncé.

On va utiliser la formule du cours avec les coordonnées :

xx’ + yy’

Pour les coordonnées du vecteur ^→BC,
on fait x’ = x_C – x_B = -2 – 2 = -4
et y’ = y_C – y_B = -1 – (-2) = 1

Pour les coordonnées du vecteur ^→AM,
on fait x = x_M – x_A = x_M – (-1) = x_M + 1
et y = y_M – y_A = y_M – 2.

On obtient donc xx’ + yy’ = 3
⇔ (x_M + 1)×(-4) + (y_M – 2)*1 = 3
⇔ -4x_M – 4 + y_M – 2 = 3
⇔ -4x_M + y_M – 6 – 3 = 0

L’ensemble D des points M est la droite d’équation cartésienne
-4x + y – 9 = 0 avec x et y les coordonnées des points de la droite.

Bonne compréhension,
Sylvain

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) La courbe représentée est celle de f ‘ (et non celle de f, attention !).
Pour savoir quand f ‘ (x) = 0, il faut regarder quand la courbe de f ‘ coupe l’axe des abscisses.
On voit que la courbe coupe l’axe des abscisses quand x = -2.
Quand x < -2, la courbe de f ‘ est en dessous de l’axe des abscisse
donc f ‘ (x) < 0.
Quand x > -2, la courbe de f ‘ est en dessous de l’axe des abscisse
donc f ‘ (x) > 0.

Pour obtenir les variations de f, faisons donc le tableau de signe de f ‘ (x) avec ces informations.

2) Pour avoir les variations de f ‘ avec le graphique, on regarde quand sa courbe monte vers la droite (soit f ‘ croissante) et quand sa courbe descend vert la droite (soit f ‘ décroissante).
On peut voir que f ‘ est croissante jusqu’à x = -1 et que f ‘ est décroissante ensuite. Soit le tableau de variation suivant :

Le signe de f ‘ ‘ (x) dépend directement de la variation de f ‘ comme indiqué dans le tableau ci-dessus.

3) Pour déterminer la convexité de f, on doit déterminer le signe de f ‘ ‘ (x) (que l’on a déjà ici) et faire une ligne en dessous avec les mots concaves / convexe / point d’inflexion.

4) La seule donnée que l’on a dans l’énoncé, c’est la courbe de f ‘. Or, les f ‘ ‘(x) sont les nombres dérivées de la fonction f ‘ : ce sont donc les coefficients directeurs des tangentes à la courbe de f ‘.

Pour calculer f ‘ ‘ (0), il faut donc tracer la tangente à la courbe de f ‘ au point d’abscisse 0 (c’est T).
Prenons deux points de T pour calculer le coefficient directeur qui est f ‘ ‘(0).

Par exemple A(0 ; 1) et B(2 ; 0).

On utilise la formule du coefficient directeur :

f ‘ ‘(0) = m = ^{(0 – 1)}/_{(2 – 0)}
= –¹/₂

5) Pour la courbe de f, d’après les tableaux, on sait que la fonction est décroissante jusqu’à -2 puis croissante. De plus, il y a un point d’inflexion en -1. C’est clairement la courbe C₁ qui convient car on voit que la pente diminue (les tangentes sont au-dessus) à partir de l’abscisse -1.

Pour la courbe de f ‘, d’après les tableaux, on sait que
f ‘ ‘(0) = –¹/₂
et que
f ‘ ‘(x) est positif avant -1 puis négatif après -1. C’est clairement C₃ qui convient, elle coupe même l’axe des ordonnées en -0.5.

6) On a vu dans le tableau de la convexité de f que le point d’inflexion est atteint en x = -1. Le seul moyen de connaître f(-1) ici est la courbe C₁.
Donc f(-1) = 0 car la courbe coupe l’axe des abscisses en x = -1.

L’équation d’une tangente au point d’abscisse a est :

Ici a = -1.

Donc y = f ‘ (-1) × (x – (-1)) + f(-1)
y = 1.35 × (x + 1) + 0
y = 1.35x + 1.35.

1.35 est une valeur approchée avec la précision permise par le graphique de la courbe de f ‘. C’est l’image de -1 par f ‘.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

A(-1 ; 4), B(-2 ; -4), D(2 ; -2) et E(5 ; 2).

1) C tel que ABCD parallélogramme :

Rédaction :

On veut ABCD parallélogramme.
Or :

Donc on veut ^→AB = ^→DC

Comme on a les coordonnées des points A et B, on peut déjà calculer les coordonnées du vecteur ^→AB avec la formule :

On peut mettre les parenthèses en ligne horizontale :
^→AB(x_B – x_A ; y_B – y_A)
soit ^→AB(-2 – (-1) ; -4 – 4)
soit ^→AB(-2 + 1 ; -8)
soit ^→AB(-1 ; -8)

De même pour ^→DC :
^→DC(x_C – x_D ; y_C – y_D)
soit ^→DC(x_C – 2 ; y_C – (-2))
soit ^→DC(x_C – 2 ; y_C + 2)

Comme les vecteurs sont égaux, leurs coordonnées sont égales. On a donc :

Pour les abscisses x :
-1 = x_C – 2
⇔ x_C – 2 = -1
⇔ x_C = -1 + 2
⇔ x_C = 1

Pour les ordonnées y :
-8 = y_C + 2
⇔ y_C + 2 = -8
⇔ y_C = -8 – 2
⇔ y_C = -10

Le point C a donc pour coordonnées (1 ; -10).
En recalculant les coordonnées du vecteur ^→DC, on vérifie qu’elles valent bien
(-1 ; -8) et qu’elles sont égalent à celles de ^→AB.

2) Centre I de ABCD :

Rédaction :

Comme I est le centre du parallélogramme ABCD, c’est le milieu des deux diagonales. En calculant les coordonnées du milieu de l’une ou l’autre des diagonales, on détermine le point I.

La formule du milieu d’un segment [AB] est :

Attention! Sur ton parallélogramme, les diagonales sont [AC] et [BD].
Calculons les coordonnées de I milieu de [BD] :

x_I = ^{(x_B + x_D)}/₂
= ^{(-2 + 2)}/₂
= ⁰/₂
= 0

y_I = ^{(y_B + y_D)}/₂
= ^{(-4 – 2)}/₂
= ^-6/₂
= -3

Les coordonnées du milieu I sont donc (0 ; -3). C’est le centre du parallélogramme.

3) J tel que ^→JA = 3^→JE :

Rédaction :

Pour déterminer les coordonnées du point J, il faut utiliser les coordonnées de vecteurs.

D’une part :
^→JA(x_A – x_J ; y_A – y_J)
soit ^→JA(-1 – x_J ; 4 – y_J)

D’autre part :
3^→JE( 3×(x_E – x_J) ; 3×(y_E – y_J))
soit 3^→JE(3×(5 – x_J) ; 3×(2 – y_J))
soit 3^→JE(15 – 3x_J ; 6 – 3y_J)

Comme les deux membres de l’égalité sont égaux, les coordonnées en x et y sont égales.

Pour les x :
-1 – x_J = 15 – 3x_J
⇔ -1 + 2x_J = 15
⇔ -1 + 2x_J + 1 = 15 + 1
⇔ 2x_J = 16
⇔ x_J = ¹⁶/₂ = 8

Pour les y :
4 – y_J = 6 – 3y_J
⇔ 4 + 2y_J = 6
⇔ 4 + 2y_J – 4 = 6 – 4
⇔ 2y_J = 2
⇔ y_J = ²/₂ = 1

Les coordonnées de J sont donc (8 ; 1).

4) B, D et J alignés :

Rédaction :

B, D et J sont alignés si et seulement si les deux vecteurs ^→BD et ^→BJ sont colinéaires. (ou deux autres avec ces trois points)

Calculons ^→BD :
^→BD(x_D – x_B ; y_D – y_B)
soit ^→BD(2 – (-2) ; -2 – (-4))
soit ^→BD(2 + 2 ; -2 + 4)
soit ^→BD(4 ; 2)
On a donc : x = 4 et y = 2.

Calculons ^→BJ :
^→BJ(x_J – x_B ; y_J – y_B)
soit ^→BJ(8 – (-2) ; 1 – (-4))
soit ^→BJ(8 + 2 ; 1 + 4)
soit ^→BJ(10 ; 5)
On a donc : x’ = 10 et y’ = 5.

« Deux vecteurs de coordonnées (x ; y) et (x’ ; y’) sont colinéaires
si et seulement si
x’ × y – x × y’ = 0. »

Calculons x’ × y – x × y’
= 10 × 2 – 4 × 5
= 20 – 20
= 0.
Le résultat vaut 0, donc les vecteurs ^→BD et ^→BJ sont égaux
donc les points B, D et J sont alignés.

5) AB, AD et BD :

Rédaction :

On cherche à calculer des distances. Il y a une formule pour ça, la voici :

AB = √[(x_B – x_A)² + (x_B – x_A)²]
= √[(-2 – (-1))² + (-4 – 4)²]
= √[(-2 + 1)² + (-8)²]
= √[(-1)² + (-8)²]
= √[1 + 64]
= √65

AD = √[(x_D – x_A)² + (x_D – x_A)²]
= √[(2 – (-1))² + (-2 – 4)²]
= √[(2 + 1)² + (-6)²]
= √[(3)² + (-6)²]
= √[9 + 36]
= √45

BD = √[(x_D – x_B)² + (x_D – x_B)²]
= √[(2 – (-2))² + (-2 – (-4))²]
= √[(2 + 2)² + (-2 + 4)²]
= √[(4)² + (2)²]
= √[16 + 4]
= √20

6) Nature du triangle ABD :

Rédaction :

On sait que AB = √65,
AD = √45
et BD = √20.

AB est le plus grand côté.
D’une part :
AB² = (√65)² = 65.
D’autre part :
AD² + BD²
= (√45)² + (√20)²
= 45 + 20
= 65.

On a bien AB² = AD² + BD².

D’après la réciproque du théorème de Pythagore, le triangle ABD est rectangle en D avec [AB] comme hypoténuse.

7) Aire du parallélogramme ABCD :

Rédaction :

Un parallélogramme est composé de deux triangles en surface. Ici le triangle ABD et le triangle BCD qui sont de même surface. On peut dire que l’aire de ABCD est le double de l’aire de ABD.
Or ABD est un triangle rectangle en D, la base et la hauteur sont donc les côtés qui bordent l’angle droit en D. On va dire que la base est AD et la hauteur BD. En effet, la base et la hauteur sont toujours perpendiculaires.

Aire_ABD = ^{(base × hauteur)}/₂
= ^{(AD × BD)}/₂
= ^{(√45 × √20)}/₂
= ^{(√(9×5) × √(4×5))}/₂
= ^{(√9 × √5 × √4 × √5)}/₂
= ^{(3 × √5 × 2 × √5)}/₂
= ^{(6 × √5 × √5)}/₂
= ^{(6 × 5)}/₂
= ⁽³⁰⁾/₂
= 15.

C’est l’aire des triangles, donc l’aire du parallélogramme ABCD est le double soit 30.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) L’effectif de la classe [17 ; 19[ est égal à 2. La surface des rectangles verticaux est proportionnelle à l’effectif de la tranche.

La surface est ici de 2 x 2 (largeur de la classe fois la hauteur). On a donc une surface de 4 pour un effectif de 2. La conséquence ici est que l’effectif fait 2 fois moins que la surface.

Pour la classe [4 ; 10[, on a une surface de 3×6 soit 18. Donc ici, l’effectif est de 9 car 2 fois moins que la surface.

Pour la classe [10 ; 12[, on a une surface de 5×2 soit 10. Ici, l’effectif est de 5 car 2 fois moins que la surface.

Pour la classe [12 ; 15[, on a une surface de 6×3 soit 18. Ici, l’effectif est de 9 car 2 fois moins que la surface.

Pour la classe [15 ; 17[, on a une surface de 5×2 soit 10. Ici, l’effectif est de 5 car 2 fois moins que la surface.

Pour la classe [19 ; 29[, on a une surface de 1×10 soit 5. Ici, l’effectif est de 5 car 2 fois moins que la surface.

2) Dans le premier échantillon, il y a un effectif N de 40.

Pour obtenir le premier quartile Q₁, il faut prendre la valeur de l’élément avec le numéro ^N/₄ (ou le premier entier au-dessus de ce nombre).

Ici ⁴⁰/₄ = 10 donc on prend la 10ème valeur qui vaut
Q₁ = 262 pour la première série.
Cela veut dire que 25% des valeurs sont inférieures ou égales à 262.

Pour la seconde série, ³⁶/₄ = 9 donc on prend la 9ème valeur qui vaut
Q₁ = 267.
Donc 25% des valeurs sont inférieures ou égales à 267.

Pour calculer Q₃, c’est l’élément numéro ^3N/₄ (ou le premier entier au-dessus de ce nombre) qu’il faut prendre puis donner sa valeur.
Soit ^3×40/₄ le 30ème pour la seconde série :
Q₃ = 266.
Pour la première série, 75% des valeurs sont inférieuresou égales à 266.

Soit ^3×36/₄ le 27ème pour la seconde série :
Q₃ = 272.
Pour la première série, 75% des valeurs sont inférieuresou égales à 272.

3) L’intervalle interquartile se calcule en faisant
Q₃ – Q₁.
Il vaut 266 – 262 = 4 pour la série 1.
Il vaut 272 – 267 = 5 pour la série 2.
Selon cet indicateur, les valeurs de la seconde série sont plus dispersées.

4) Pour le diagramme en boîte, il faut faire un rectangle qui commence à Q₁ à gauche et qui finit à Q₃ à droite.

Sur les côtés du rectangle, on trace deux traits horizontaux qui vont vers le minimum et le maximum à partir du rectangle. On met un gros point sur ces valeurs.

5) D’après la diagramme ci-dessus, la machine qui semble la plus appropriée est celle dont la boîte (le rectangle) se resserre autour de la valeur médiane voulue, soit 265. C’est donc la première machine pour laquelle la boîte Q1/Q3 contient la médiane Me = 265.

6) La moyenne d’une série statistique est :

Faisons un tableau d’effectifs avec les valeurs de la second série :

La moyenne est donc d’environ 269,9722 soit environ 269,97 à 0.01 près.

La variance indique la dispersion des valeurs autour de la moyenne. Sa formule est :

V = ( n₁(x₁ – ^–x)² + n₂(x₂ – ^–x)² + … + n_P(x_P – ^–x)² ) / (n₁ + n₂ + … + n_P)

J’ai donc calculé le numérateur avec ce grand tableau.

D’abord, je calcule les carrés des différences en passant de gauche à droite. Ensuite, je calcule la somme totale du numérateur.

Enfin, j’obtiens la variance en divisant le numérateur 766.9724 par l’effectif total 40.
Cela donne V = ^766.9724/₄₀ = 21.3048 environ.

Un calculateur internet (ou votre calculatrice) me retourne une variance de 21.9135. Il a surement considéré une moyenne de 269,9722 (quatre chiffres après la virgule) alors que j’ai utilisé 269,97 (deux chiffres après la virgule) pour expliquer le calcul à la main avec les 18 lignes.

Si le nombre de lignes de calcul est de 5 ou 10, il vaut donc mieux utiliser 4 chiffres après la virgule pour la précision de la moyenne.

L’écart-type σ est la racine de la variance. Il indique aussi à quel point les valeurs sont dispersées. On utilise la racine car on avait mis des carrés pour la variance.

σ = √V
σ = √21.3048
σ = 4.6157 environ.

L’écart-type calculé est d’environ 4.6157.

Le calculateur internet (ou votre calculatrice) me retourne un écart-type de 4.6812. Il a surement considéré une moyenne de 269,9722 (quatre chiffres après la virgule) alors que j’ai utilisé 269,97 (deux chiffres après la virgule) pour expliquer le calcul à la main avec les 18 lignes.

Si le nombre de lignes de calcul est de 5 ou 10, il vaut donc mieux utiliser 4 chiffres après la virgule pour la précision de la moyenne.

Bonne compréhension,
Sylvain Jeuland

Exercice :

Tout le corrigé :

1) D’après la courbe, f est décroissante de -infini à 0 . Cela fait une flèche qui descend jusqu’à x = 0. En bas à droite de la flèche, mets la valeur de f(0) : -2,5. Ensuite, la courbe remonte donc f est croissante de 0 à +infini. La flèche du tableau de variation remonte vers la droite.

2) f'(0) est la pente la tangente à la courbe en x = 0. En x = 0, la tangente est horizontale donc sa pente est nulle et f'(0) = 0.

3) f'(x) = 0 quand la pente de la courbe (ou plutôt la pente de la tangente) est nulle, donc la courbe est horizontale (ou sa tangente). Oui, f'(x) représente une pente! Ici, la pente est horizontale en C et en B. Leurs abscisses x sont donc 0 et 6 : ce sont les solutions.

4) La tangente à la courbe Cf passant par A passe aussi par M. Pour avoir son équation (de droite), il faut déterminer son coefficient directeur avec a = (yM – yA)/(xM – xA) = (3 – 0)/(-3 -(-2))= 3/(-1) = -3. Prends y = ax + b et remplacer par des x et y que tu connais, par exemple xA et yA. Remplace aussi le coefficient directeur « a » par 3 : 0 = -3*(-2) + b. Tu obtiens b = -6. L’équation de la tangente est donc y = -3x – 6 et f'(-2), la pente de la tangente en x = -2, est -3.

5) Déjà, on doit trouver l’équation de la tangente à Cf au point D. On sait que son coefficient directeur est f'(2) = 3/4. En remplaçant dans l’équation y = ax + b par les coordonnées yD = -3/2 et xD = 2, ainsi que la pente 3/4, on obtient : -3/2 = 3/4 * 2 + b. Du coup, b = -3/2 – 3/2 = -3. L’équation de cette tangente est y = (3/4)x – 3. L’intersection avec l’axe des abcisses a lieue quand y = 0. Soit 0 = (3/4)x – 3. Cela donne x = 4.

6) C’est la courbe C2, car une fonction est décroissante quand sa dérivée est négative.
C’est le cas pour C2 qui est en dessous de l’axe y = zéro pour des x négatifs. De même, une fonction est croissante quand sa dérivée est positive.
C’est le cas pour C2 qui est au dessus de l’axe y = zéro pour des x positifs. De plus, C2 coupe l’axe des abscisses en 0 et 6, ce qui des tangentes horizontale pour Cf. Les autres coupes ne fonctionnent pas, elle ne sont pas négatives avant x = 0, puis positives après x = 0.

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) L’unité d’aire est de 3 cases, donc 3 cases représente un effectif de 1.
On obtient donc le tableau suivant :

3) L’effectif de la classe est
N = 1 + 2 + 6 + 2 + 1 + 4 + 2 + 3 + 1 + 1 = 23.

4) La moyenne x-barre = ^{(n₁ × x₁ + n₂ × x₂ + … n_P × x_P)}/_N
= ^{(1 × 5 + 2 × 6 + … + 1 × 19)}/₂₃
= ²⁵⁰/₂₃ = 10.9 au dixième de point près.

5) Pour avoir le pourcentage des élèves qui ont eu 8 ou moins, on compte les effectifs. Soit 1 + 2 + 6 = 9.
Comme 100% correspond à 23 individus, on fait un tableau de proportionnalité avec :
23 | 100 %
9 | x %.
Le produit en croix donne x = 9×100/23 = 39% au pourcent près.

6) Pour obtenir une médiane, il faut tout d’abord faire le tableau des effectifs cumulés croissants (ECC).

L’effectif total est de 23, c’est un nombre impair donc il n’y a qu’une seule valeur centrale : la 12ème (²³/₂ = 11.5 et on prend donc la valeur suivante).

D’après le tableau des ECC, la 12ème valeur est la note 11. Donc la médiane Me est égale à 11.

Au moins la moitié des valeurs sont donc inférieures ou égales à 11 et au moins la moitié des valeurs sont supérieures ou égales à 11.

7) Pour obtenir Q1, on fait 0.25×N = 0.25×23 = 5.75. Q1 est donc la 6ème valeur qui est la note 8. Q1 = 8.

Au moins un quart des valeurs sont donc inférieures ou égales à 8.

Pour obtenir Q3, on fait 0.75×N = 0.75×23 = 17.25. Q3 est donc la 18ème valeur qui est la note 13. Q3 = 13.

Au moins 75% des valeurs sont donc inférieures ou égales à 13.

8) La valeur minimale est 5, la valeur maximale est 19, on a Q1, Q3 et Me, on peut donc dessiner le diagramme en boîte appelé boîte à moustache.

* Environ la moitié des élèves ont une note entre 8 et 13.

* Environ les trois-quarts des élèves ont au dessus de 8.

* Environ un quart des élèves ont une note au dessus de 13.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit sur l’exercice

Tout le corrigé :

1) On voit que le plan (IJK) descend en biais et traverse le plan (BCF) en K.
On sait que (IJ) et (EF) sont parallèles d’après l’énoncé.

On utilise le « théorème du toit ».

Soit (P) un plan contenant une droite (d) et (P’) contenant une droite (d’) parallèle à (d). Si les deux plans (P) et (P’) sont sécants alors leur intersection est une droite parallèle à (d).

Le plan (IJK) contient la droite (IJ) et le plan (BCF) à droite contient la droite (EF). De plus, (EF) est parallèle à (IJ). Ces deux plans sont sécants (en K notamment) donc d’après le théorème du toit leur intersection est une droite parallèle à (IJ). On appelle D cette droite d’intersection (le gros trait rouge ci-dessous).

2) On sait que (D) est parallèle à (IJ) donc à (EF). K est à la fois sur (IJK) et (BCF). Il faut donc tracer (D) passant par K parallèle à (EF). On obtient deux points qui sont appelés L et M sur les bords de la face BCEF : L est sur la droite (EB) et M est sur la droite (FC).

Attention : mon trait rouge passant par le point K est un peu trop bas !!! Je l’ai fait passer par la lettre.

Le plan (IJK) coupe la face frontale ABED par le point I et par le point L. Donc on trace la droite (IL).
Le plan (IJK) coupe la face de derrière ACFD par le point J et par le point M. Donc on trace la droite (JM).

(IL) et (AB) sont deux droites sécantes dans le plan frontal (ABD). Leur point d’intersection appartient donc aux droites (IL) et (AB). On sait que (IL) appartient au plan (IJK) et (AB) appartient au plan (ABC). Donc l’intersection de (IL) et (AB) appartient à la droite d’intersection des plans (IJK) et (ABC). On trouve ce point en prolongeant les droites. Appelons-le R.

(JM) et (AC) sont deux droites sécantes dans le plan de derrière (ACD). Leur point d’intersection appartient donc aux droites (JM) et (AC). On sait que (JM) appartient au plan (IJK) et (AC) appartient au plan (ABC). Donc l’intersection de (JM) et (AC) appartient à la droite d’intersection des plans (IJK) et (ABC). On trouve ce point en prolongeant les droites. Appelons-le S.

Deux plans sécants ont une droite pour intersection. Nous avons deux points distincts R et S qui appartiennent aux deux plans (IJK) et (ABC), donc à leur intersection. Du coup, (RS) forment la droite d’intersection de ces deux plans. Il est possible de la tracer.

3)

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers le corrigé

Tout le corrigé :

1) Pour tracer les droites d’équations y = x
et y = 0.85x + 1.8, on choisit deux valeurs de x (ici 0 et 10) puis on calcule leurs images y. Cela donne deux points de coordonnées x et y que l’on place. On trace l’unique droite qui passe par ces deux points.

2) Partons du u₀ et déterminons les autres termes par ricochet sur les deux droites. La droite y = 0.85x + 1.8 représente la suite u_n+1 = 0.85u_n + 1.8.

3) Comme l’intersection des deux droites se fait pour x = 12, et que les segments des u_n semblent aller vers cette intersection, je conjecture que la limite de la suite est 12.

4) On a pour tout n entier naturel, v_nn – 12.
On sait aussi que u_n+1 = 0,85×u_n + 1.8.

Pour prouver qu’une suite (v_n) est géométrique, il faut arriver à :
Pour tout n entier naturel, v_n+1 = q*v_n, donc on écrit sur la feuille :

Pour tout n entier naturel,
v_n+1 = u_n+1 – 12 (on fait appel à l’égalité entre v_n et u_n)
= 0,85×u_n + 1.8 – 12 (on fait appel à l’égalité entre u_n+1 et u_n)
= 0,85×u_n – 10,2
= 0,85×( u_n – 10,2/0,85 ) (on factorise par le coefficient devant u_n)
= 0,85×( u_n – 10,2/0,85 )
= 0,85×( u_n – 12 )
= 0,85×v_n (on refait appel à l’égalité entre u_n+1 et u_n dans l’autre sens)

Il existe un réel q réel (q = 0,85), tel que pour tout n entier naturel,
v_n+1 = q×v_n,
donc (v_n) est une suite géométrique de raison 0,85 et de premier terme v₀
= u₀ – 12
= 8 – 12
= -4.

5) Comme (v_n) est géométrique, on utilise la formule explicite (qui dépend de n),
v_n = v_p×q^n-p avec p = 0 comme on commence à 0.

Du coup, pour tout n, v_n
= v₀×qⁿ = -4×0,85ⁿ.

Comme v_n = u_n – 12,
alors u_n = v_n + 12
= -4×0,85ⁿ + 12
= 12 – 4×0,85ⁿ.

6) Pour obtenir le sens de variation d’une suite, il faut déterminer le signe de
u_n+1 – u_n. S’il est positive, la suite est croissante. S’il est négatif, la suite est décroissante.

Pour tout n réel, u_n+1 – u_n
= 12 – 4×0,85ⁿ⁺¹ – [12 – 4×0,85ⁿ] (on n’oublie pas les crochets après le « moins »)
= 12 – 4×0,85ⁿ⁺¹ – 12 + 4×0,85ⁿ (les 12 s’annulent)
= – 4×0,85ⁿ⁺¹ + 4×0,85ⁿ
= 4×0,85ⁿ – 4×0,85ⁿ⁺¹
= 4×[ 0,85ⁿ – 0,85ⁿ⁺¹ ] (on factorise par 4)
= 4×[ 0,85ⁿ – 0,85ⁿ × 0,85 ] (les puissances : aⁿ⁺¹ = aⁿ × a¹ = aⁿ × a)
= 4×[ 0,85ⁿ × 1 – 0,85ⁿ × 0,85 ]
= 4×[ 0,85ⁿ × (1 – 0,85) ] (on factorise par 0,85ⁿ)
= 4×[ 0,85ⁿ × 0,15 ].

4 est positif, 0,85ⁿ est positif, 0,15 est positif. D’après la règle des signes avec ce produit,
Pour tout n réel, u_n+1 – u_n > 0.
Donc la suite (u_n) est strictement croissante.

7) u_n = 12 – 4*0,85ⁿ
lim_n→+∞ 0,85ⁿ = 0 car 0 < 0,85 < 1,
Par produit, lim_n→+∞ 4×0,85ⁿ = 0 car 4*0,

Par somme, lim_n→+∞ (12 – 4×0,85ⁿ) = 0 car 12-0,

Donc la limite de la suite est 12.

8) On prend le nombre actuel d’abonnés u_n, on lui applique une baisse de 15% (coefficient multiplicateur de 0,85) donc on obtient 0,85×u_n.
Puis on ajoute 1800, soit 1,8 millier, cela donne 0,85×u_n + 1,8.
On obtient le nombre suivant d’abonnés qui est u_n+1.
Du coup, on a pour tout n entier naturel u_n+1 = 0,85×u_n + 1,8.
Sans oublier que u₀ = 8, ce qui correspond au 8000 de 2008.
Cette situation peut donc être modélisée par la suite (u_n).

9) 2014, c’est 2008+6 soit 2008+n pour n=6.
Il faut donc calculer
u₆ = 12 – 4×0,85⁶ = 10,4914, soit un nombre d’abonnés de 10491 en 2014.

Exercice : Clic droit sur l’exercice

Tout le corrigé :

1) Pour passer de 2010 à 2011, on fait une baisse de 15%. Le coefficient multiplicateur de baisse de 15% est de (1 – ¹⁵/₁₀₀) = 0,85. Pour calculer le nouveau nombre de 2011, on multiplie donc par 0,85.

Pour revenir de la valeur de 2011 à celle de 2010, il faut effectuer l’opération inverse, soit diviser par le coefficient multiplicateur de baisse de 15%, donc on divise par 0,85.

Ce qui fait un coefficient multiplicateur de retour de ¹/_0,85 soit environ 1,176.
Pour retrouver le pourcentage correspondant on fait deux opérations :
1,176 – 1 = 0,176.
0,176 × 100 = 17,6%.

La population doit donc remonter de 17,6% pour retrouver le prix initial.

2) Si avec 10 euros, j’achète une quantité x de chocolat et que le marchand me donne 40% +, c’est que j’obtiens une quantité 1.40x car le coefficient multiplicateur est (1 – ⁴⁰/₁₀₀).

Avec un tableau de proportionnalité, nous pouvons déterminer le prix correspondant à la quantité x alors 10 euros correspond à 1.40x :
10 euros correspond à la quantité 1.40x
?? euros correspond à la quantité x

On fait un produit en croix et on obtient :
?? = ^{(10 × x)}/_(1.40x)
?? = ¹⁰/_1.40 = 7,1428 euros.

Le prix de la quantité x revient donc à environ 7.1428 euros.
Le prix initial était de 10. Le prix final est de 7.1428.

Pour calculer un coefficient multiplicateur CM, on fait :
Valeur initiale × CM = Valeur finale
soit 10 × CM = 7.1428
soit CM = 7.1428/10 = 0.71428.

Pour retrouver le pourcentage de baisse, on effectue
les opérations – 1 et × 100.
0.71428 – 1 = -0.28572
-0.28572 × 100 = -28.572%.

Le pourcentage de baisse est de 28.572%.

3) Il faut mettre 100 sous la valeur de 2007 car c’est la valeur initiale et l’indice est de base 100. Puis il faut faire les produits en croix par rapport à la première colonne pour trouver les autres valeurs.

^{35.5 × 100}/_9.4 = 377.66 pour 2007,
^{104.5 × 100}/_9.4 = 1111,70 pour 2008,
^{268 × 100}/_9.4 = 2851.06 pour 2009.

Donc le tableau est :
Années : 2006 | 2007 | 2008 | 2009
Marché en (MW) : 9.4 | 35.5 | 104.5 | 268
Indices : 100 | 377.66 | 1111.70 | 2851.06

4-5) Pour les taux de croissance, on calcule les coefficients multiplicateurs en divisant les indices d’arrivée par les indices de départ.

4) Pour calculer un coefficient multiplicateur CM₁ de 2007 à 2009, on effectue l’opération :
CM₁ = ^{(Valeur arrivée)}/_{(Valeur départ)}
= ^1111.70/₁₀₀
= 11.1170.

Pour trouver les taux à partir des coefficients multiplicateurs, on fait les opérations -1 et × 100.

11.1170 – 1 = 10.1170.
10.1170 × 100 = +1011.70%

L’augmentation de 2007 à 2009 est de +1011.70%.

5) Pour calculer un coefficient multiplicateur CM₂ de 2006 à 2007, on effectue l’opération :
CM₂ = ^{(Valeur arrivée)}/_{(Valeur départ)}
= ^377.66/₁₀₀
= 3.7766.

Pour trouver les taux à partir des coefficients multiplicateurs, on fait les opérations -1 et × 100.

3.7766 – 1 = 2.7766.
2.7766 × 100 = +277.66%.

L’augmentation de 2006 à 2007 est de +277.66%

6) La côte de popularité est passée de 50 à 45%.
Pour calculer un coefficient multiplicateur CM₃, on effectue l’opération :
CM₃ = ^{(Valeur arrivée)}/_{(Valeur départ)}
= ⁴⁵/₅₀
= 0.90.

Pour trouver les pourcentages de hausse et de baisse à partir des coefficients multiplicateurs, on fait les opérations -1 et × 100.

0.90 – 1 = -0.10.
-0.10 × 100 = -10%.

La baisse est de +10%. La perte de points n’est pas égale au pourcentage de baisse. Je ne suis pas d’accord avec ce commentaire.

7) 1000 personnes ont été interrogées.

Lors du premier sondage, la côte de popularité est de 50%.
Donc le nombre de satisfaits est de
⁵⁰/₁₀₀ × 1000 = 500 personnes étaient satisfaites avant.

Lors du seconde sondage, la côte de popularité est de 450%.
Donc le nombre de satisfaits est de
⁴⁵/₁₀₀ × 1000 = 450 personnes sont satisfaites maintenant.

Le pourcentage de baisse (la formule sans le calcul du coefficient multiplicateur) est :
^{(Valeur2 – Valeur1)}/_Valeur1 × 100
= ^{(450 – 500)}/₅₀₀ × 100
= ^-50/₅₀₀ × 100
= -0,1 × 100
= -10%.

Soit une baisse de 10%. Cela correspond bien à la première question.

8) La côte gagne 5 points.

Le pourcentage de hausse (la formule sans le calcul du coefficient multiplicateur) est :
^{(Valeur2 – Valeur1)}/_Valeur1 × 100
= ^{(40 – 35)}/₃₅ × 100
= ⁵/₃₅ × 100
= 0,1428 × 100
= 14.28%.

La hausse est de 14.28%.

Bonne compréhension,
Sylvain Jeuland