frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

A(-1 ; 4), B(-2 ; -4), D(2 ; -2) et E(5 ; 2).

1) C tel que ABCD parallélogramme :

Rédaction :

On veut ABCD parallélogramme.
Or :

Donc on veut ^→AB = ^→DC

Comme on a les coordonnées des points A et B, on peut déjà calculer les coordonnées du vecteur ^→AB avec la formule :

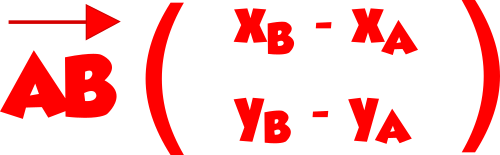
On peut mettre les parenthèses en ligne horizontale :
^→AB(x_B – x_A ; y_B – y_A)
soit ^→AB(-2 – (-1) ; -4 – 4)
soit ^→AB(-2 + 1 ; -8)
soit ^→AB(-1 ; -8)

De même pour ^→DC :
^→DC(x_C – x_D ; y_C – y_D)
soit ^→DC(x_C – 2 ; y_C – (-2))
soit ^→DC(x_C – 2 ; y_C + 2)

Comme les vecteurs sont égaux, leurs coordonnées sont égales. On a donc :

Pour les abscisses x :
-1 = x_C – 2
⇔ x_C – 2 = -1
⇔ x_C = -1 + 2
⇔ x_C = 1

Pour les ordonnées y :
-8 = y_C + 2
⇔ y_C + 2 = -8
⇔ y_C = -8 – 2
⇔ y_C = -10

Le point C a donc pour coordonnées (1 ; -10).
En recalculant les coordonnées du vecteur ^→DC, on vérifie qu’elles valent bien
(-1 ; -8) et qu’elles sont égalent à celles de ^→AB.

2) Centre I de ABCD :

Rédaction :

Comme I est le centre du parallélogramme ABCD, c’est le milieu des deux diagonales. En calculant les coordonnées du milieu de l’une ou l’autre des diagonales, on détermine le point I.

La formule du milieu d’un segment [AB] est :

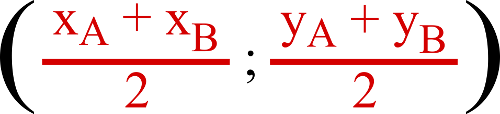
Attention! Sur ton parallélogramme, les diagonales sont [AC] et [BD].
Calculons les coordonnées de I milieu de [BD] :

x_I = ^{(x_B + x_D)}/₂
= ^{(-2 + 2)}/₂
= ⁰/₂
= 0

y_I = ^{(y_B + y_D)}/₂
= ^{(-4 – 2)}/₂
= ^-6/₂
= -3

Les coordonnées du milieu I sont donc (0 ; -3). C’est le centre du parallélogramme.

3) J tel que ^→JA = 3^→JE :

Rédaction :

Pour déterminer les coordonnées du point J, il faut utiliser les coordonnées de vecteurs.

D’une part :
^→JA(x_A – x_J ; y_A – y_J)
soit ^→JA(-1 – x_J ; 4 – y_J)

D’autre part :
3^→JE( 3×(x_E – x_J) ; 3×(y_E – y_J))
soit 3^→JE(3×(5 – x_J) ; 3×(2 – y_J))
soit 3^→JE(15 – 3x_J ; 6 – 3y_J)

Comme les deux membres de l’égalité sont égaux, les coordonnées en x et y sont égales.

Pour les x :
-1 – x_J = 15 – 3x_J
⇔ -1 + 2x_J = 15
⇔ -1 + 2x_J + 1 = 15 + 1
⇔ 2x_J = 16
⇔ x_J = ¹⁶/₂ = 8

Pour les y :
4 – y_J = 6 – 3y_J
⇔ 4 + 2y_J = 6
⇔ 4 + 2y_J – 4 = 6 – 4
⇔ 2y_J = 2
⇔ y_J = ²/₂ = 1

Les coordonnées de J sont donc (8 ; 1).

4) B, D et J alignés :

Rédaction :

B, D et J sont alignés si et seulement si les deux vecteurs ^→BD et ^→BJ sont colinéaires. (ou deux autres avec ces trois points)

Calculons ^→BD :
^→BD(x_D – x_B ; y_D – y_B)
soit ^→BD(2 – (-2) ; -2 – (-4))
soit ^→BD(2 + 2 ; -2 + 4)
soit ^→BD(4 ; 2)
On a donc : x = 4 et y = 2.

Calculons ^→BJ :
^→BJ(x_J – x_B ; y_J – y_B)
soit ^→BJ(8 – (-2) ; 1 – (-4))
soit ^→BJ(8 + 2 ; 1 + 4)
soit ^→BJ(10 ; 5)
On a donc : x’ = 10 et y’ = 5.

“Deux vecteurs de coordonnées (x ; y) et (x’ ; y’) sont colinéaires
si et seulement si
x’ × y – x × y’ = 0.”

Calculons x’ × y – x × y’
= 10 × 2 – 4 × 5
= 20 – 20
= 0.
Le résultat vaut 0, donc les vecteurs ^→BD et ^→BJ sont égaux
donc les points B, D et J sont alignés.

5) AB, AD et BD :

Rédaction :

On cherche à calculer des distances. Il y a une formule pour ça, la voici :

AB = √[(x_B – x_A)² + (x_B – x_A)²]
= √[(-2 – (-1))² + (-4 – 4)²]
= √[(-2 + 1)² + (-8)²]
= √[(-1)² + (-8)²]
= √[1 + 64]
= √65

AD = √[(x_D – x_A)² + (x_D – x_A)²]
= √[(2 – (-1))² + (-2 – 4)²]
= √[(2 + 1)² + (-6)²]
= √[(3)² + (-6)²]
= √[9 + 36]
= √45

BD = √[(x_D – x_B)² + (x_D – x_B)²]
= √[(2 – (-2))² + (-2 – (-4))²]
= √[(2 + 2)² + (-2 + 4)²]
= √[(4)² + (2)²]
= √[16 + 4]
= √20

6) Nature du triangle ABD :

Rédaction :

On sait que AB = √65,
AD = √45
et BD = √20.

AB est le plus grand côté.
D’une part :
AB² = (√65)² = 65.
D’autre part :
AD² + BD²
= (√45)² + (√20)²
= 45 + 20
= 65.

On a bien AB² = AD² + BD².

D’après la réciproque du théorème de Pythagore, le triangle ABD est rectangle en D avec [AB] comme hypoténuse.

7) Aire du parallélogramme ABCD :

Rédaction :

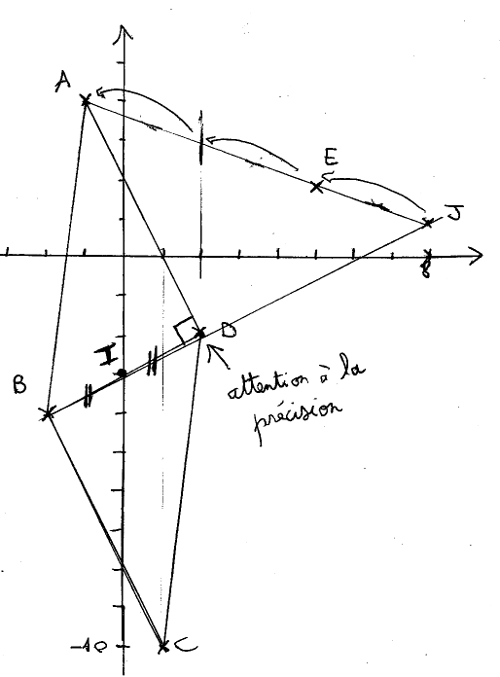
Un parallélogramme est composé de deux triangles en surface. Ici le triangle ABD et le triangle BCD qui sont de même surface. On peut dire que l’aire de ABCD est le double de l’aire de ABD.
Or ABD est un triangle rectangle en D, la base et la hauteur sont donc les côtés qui bordent l’angle droit en D. On va dire que la base est AD et la hauteur BD. En effet, la base et la hauteur sont toujours perpendiculaires.

Aire_ABD = ^{(base × hauteur)}/₂
= ^{(AD × BD)}/₂
= ^{(√45 × √20)}/₂
= ^{(√(9×5) × √(4×5))}/₂
= ^{(√9 × √5 × √4 × √5)}/₂
= ^{(3 × √5 × 2 × √5)}/₂
= ^{(6 × √5 × √5)}/₂
= ^{(6 × 5)}/₂
= ⁽³⁰⁾/₂
= 15.

C’est l’aire des triangles, donc l’aire du parallélogramme ABCD est le double soit 30.

Bonne compréhension,
Sylvain Jeuland