Exercice de maths de seconde sur la géométrie avec distance, triangle, repère, coordonnées de point, milieu, triangle, abscisse, ordonnée.
Exercice N°219 :
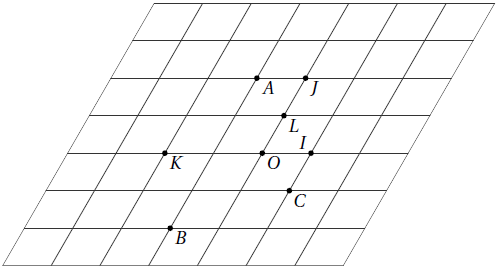
1) Quelles sont les coordonnées de A, B et C dans le repère (O, I, J) ? Lis la suite »
Géométrie 2D – Repère, milieu, triangle, distance, cercle – Seconde
24 septembre 2020
Géométrie 2D – Repère, coordonnées, milieux, distances – Seconde
24 septembre 2020
Exercice de maths de seconde sur la géométrie avec coordonnées, milieu, distance. Répère du plan, segment, abscisse, ordonnée, cercle.
Exercice N°218 :
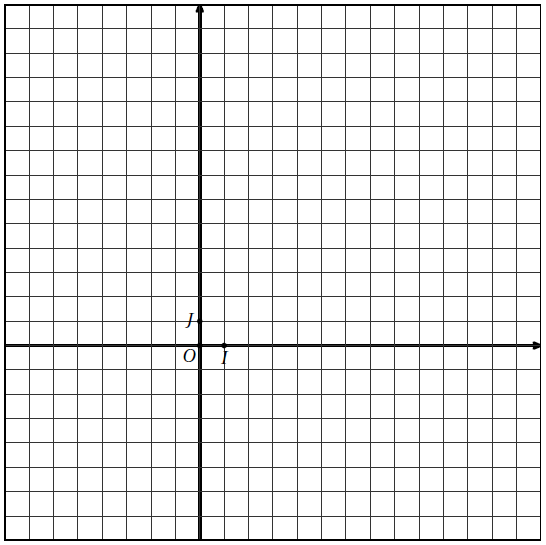
Soit (O, I, J) un repère orthonormé du plan.
On définit A(1 ; −6) et B(7 ; 12).
Soit le point S le milieu du segment [AB] et C le cercle de centre S passant par A.
1) Déterminer les coordonnées du point S et le rayon R du cercle C. Lis la suite »
Géométrie 2D – Etude d’un triangle rectangle – Seconde
24 septembre 2020
Exercice de géométrie sur un triangle rectangle avec médiane, hauteur, orthocentre, cercle circonscrit, centre de gravité, distances.
Exercice N°013 :
On considère le triangle ABC dont les côté mesurent AB = 8, BC = 15, AC = 17 (en cm) ; (BM) est une médiane et (BH) une hauteur du triangle ABC
.
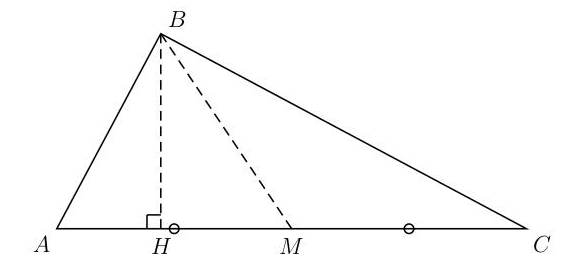
1) Montrer que le triangle ABC est rectangle en B . Lis la suite »
Arithmétique – Diviseurs, décomposition, facteurs premiers – Seconde
23 septembre 2020
Maths de seconde sur l’arithmétique avec liste de diviseurs, exercice avec décomposition en facteurs premiers, produit, carré.
Exercice N°640 :
Exercice N°640 :
1) Le nombre 403 est-il premier ? Justifier. Lis la suite »
Arithmétique – Nombres premiers, diviseurs, facteurs – Seconde
23 septembre 2020
Exercices de maths de seconde sur l’arithmétique, les nombres premiers, liste de diviseurs, décomposition en facteurs, multiple
Exercice N°639 :
Exercice N°639 :
Toutes les questions de cet exercice sont des questions indépendantes les unes des autres.
1) Déterminer le PGCD (c’est-à-dire Plus Grand Commun Dénominateur) des nombres 2520 et 2646.
2) Le nombre 251 est-il un nombre premier ? Bien justifier la réponse.
3) Le nombre 257 est-il un nombre premier ? Bien justifier la réponse.
4) Décomposer le nombre entier 980 en produit de facteurs premiers.
5) Décomposer le nombre entier 630 en produit de facteurs premiers.
6) Démontrer que la somme de deux multiples du nombre a est un multiple du nombre a.
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de Seconde de ce chapitre Ensemble de Nombres et Arithmétique (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : exercices, arithmétique, seconde, premiers.
Exercice précédent : Valeur absolue – Équation, inéquation, intervalle, distance – Seconde
Corrigé
22 septembre 2020
Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) 
2) En utilisant la formule du milieu de seconde :
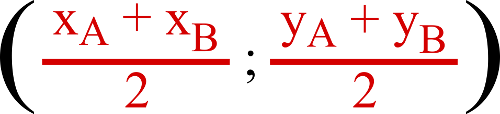
Pour les abscisses seulement ici :
a2 = (a0 + a1)/2
= (0 + 1)/2
= 1)/2
a3 = (a1 + a2)/2
= (0.5 + 1)/2
= 1.5/2
= 0.75
= 3/4
a4 = (a2 + a3)/2
= (0.5 + 0.75)/2
= 1.25/2
= (5/4)/2
= 5/8
a5 = (a3 + a4)/2
= (3/4 + 5/8)/2
= (6/8 + 5/8)/2
= (11/8)/2
= 11/16
a6 = (a4 + a5)/2
= (5/8 + 11/16)/2
= (10/16 + 11/16)/2
= (21/16)/2
= 21/32
3) C’est la formule du milieu pour les abscisses. An+2 est le milieu de An et An+1 donc on fait la demi-somme (comme la formule de la question 3) avec an et an+1 comme abscisses pour obtenir l’abscisse an+2.
4) Initialisation :
D’une part (membre de gauche),
a1 = 1.
D’autre part (membre de droite),
(-1/2)a0 + 1
= (-1/2) × 0 + 1 = 1.
On a bien :
a1 = (-1/2)a0 + 1
La propriété est vraie au rang n = 0.
Hérédité :
On suppose que la propriété est vraie au rang k. On a donc :
ak+1 = (-1/2)ak + 1
Montrons qu’elle est vraie au rang k+1, c’est à dire que
ak+2 = (-1/2)ak+1 + 1.
On sait que ak+2 = (ak + ak+1)/2
J’ai ak+2 en fonction de ak alors que je le veux en fonction de ak+1. Donc il faut remplacer le ak par du ak+1 dans le calcul.
On sait que ak+1 = (-1/2)ak + 1
Donc ak+1 – 1 = (-1/2)ak
Et (-2) × (ak+1 – 1) = ak (en multipliant par -2 de chaque côté).
D’où ak+2 = (ak + ak+1)/2
= ((-2) × (ak+1 – 1) + ak+1)/2
= (-2ak+1 + 2 + ak+1)/2
(en développant le (-2))
= (-1ak+1 + 2)/2
= (-1/2)ak+1 + 1
(en séparant les fractions « diviser par 2 », et comme 2/2 = 1).
La propriété est donc bien vraie au rang k+1. L’hérédité est prouvée.
Conclusion :
Comme j’ai prouvé l’initialisation et l’hérédité, la propriété est vraie pour tout n.
5) Pour tout n entier naturel,
vn+1 = an+1 – 2/3
= (-1/2)an + 1 – 2/3
= (-1/2)an + 1/3
= (-1/2) × [ an + (1/3)/(–1/2)]
= (-1/2) × [ an + 1/3 × (-2)]
= (-1/2) × [ an – 2/3]
= (-1/2) × vn
Il existe q ∈ R (q = –1/2) tel que pour tout n ∈ N :
vn+1 = q × vn,
donc la suite (vn) est géométrique de raison q = –1/2 et de premier terme
v0 = a0 – 2/3
= 0 – 2/3 = –2/3.
6) La formule explicite d’une suite suite géométrique est :
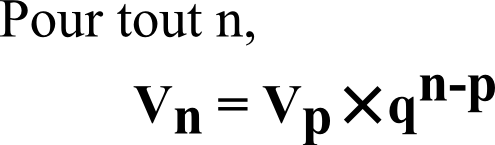
Donc vn = v0 × qn – 0
= (-2/3) × (-1/2)n
lim[n→+∞] (-1/2)n = 0 car 0 < q < 1.
Par produit, lim[n→+∞] (-2/3) × (-1/2)n = 0 (car –2/3 × 0 = 0).
D’après les données : vn = an – 2/3.
Donc an = vn + 2/3
Du coup, par somme, lim[n→+∞] an = 2/3 (car 0 + 2/3).
Bonne compréhension,
Sylvain Jeuland
Livre de maths de seconde – La variable de nombre réel – Pages 14-15
21 septembre 2020
Complexes – Équations, puissance, conjugué, fraction – Terminale
21 septembre 2020
Maths de terminale : exercice sur complexe avec fraction, conjugué, équation, produit, parties réelle et imaginaire, ensembles, solutions.
Exercice N°496 :
Exercice N°496 :
1-2-3-4-5) Questionnaire à Choix Unique, justifier et choisir la bonne réponse :
1) Le nombre 1/(√5 – i√2) est égal à :
a) (√5 + √2)/3, Lis la suite »
Graphes – Degré, chaîne eulérienne, nombre chromatique – Terminale
20 septembre 2020
Exercice de maths de terminale sur les graphes, avec degré, sommet, arête, connexité, chaîne eulérienne, nombre chromatique, tableau.
Exercice N°466 :
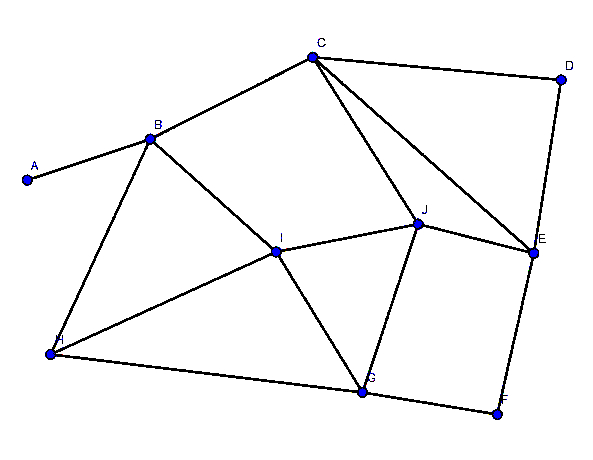
On considère le graphe ci-dessus.
1) Ce graphe est-il connexe ? Lis la suite »
Probabilités – Feux tricolores au carrefour – Première
20 septembre 2020
Exercice de probabilité sur un feu tricolore. Maths de première, arbre pondéré, répétition d’événement indépendant, loi, événement contraire.
Exercice N°020 :
Exercice N°020 :
Le cycle des feux tricolores au carrefour est le suivant :
– l’événement V : « Le feu est vert. » dure 20 secondes.
– l’événement O : « Le feu est orange. » dure 5 secondes.
– l’événement R : « Le feu est rouge. » dure 35 secondes.
Le temps total d’un cycle est donc de 1 minute.
1) Déterminer P(V). Lis la suite »
