Exercice de géométrie sur un triangle rectangle avec médiane, hauteur, orthocentre, cercle circonscrit, centre de gravité, distances.
Exercice N°013 :
On considère le triangle ABC dont les côté mesurent AB = 8, BC = 15, AC = 17 (en cm) ; (BM) est une médiane et (BH) une hauteur du triangle ABC
.
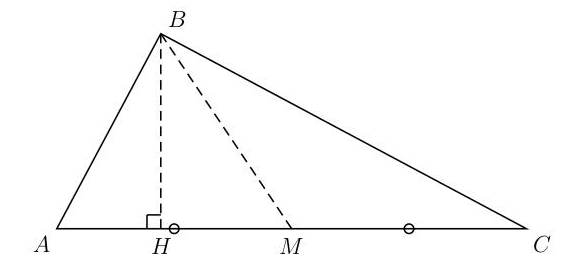
1) Montrer que le triangle ABC est rectangle en B .
2) En déduire la position de son orthocentre.
3) Donner son aire, en cm².
4) En déduire la valeur exacte, sous la forme d’une fraction, de la hauteur BH (on pourra calculer l’aire de ABC d’une autre manière).
5) Préciser la position du centre de son cercle circonscrit.
6) Donner également la valeur exacte de la médiane BM .
7) En déduire, sous forme d’une fraction, la distance BG ou G est le centre de gravité de ABC.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, géométrie, triangle rectangle.
Exercice précédent : Géométrie 2D et Algorithmique – Milieux et distances – Seconde

