Essaie les exercices de DS, clique ci-dessous
Exercice de maths de terminale de fonction avec polynôme, rationnelle, variation, continuité, équation, dérivées, limites, TVI, courbe.
Exercice N°232 :
Soit g la fonction définie sur R par
g(x) = x3 – 3x – 3.
1) Démontrer que l’équation
g(x) = 0
a une solution unique α dans R. Lis la suite »
Exercice de maths de terminale de fonction avec tan, dérivée, tangente. Trigonométrie, limite, variation, étude de signe, inéquation.
Exercice N°231 :
Soit f la fonction définie sur I = ] –π/2 ; π/2 [ par
f(x) = tan x – x – x3/3.
On appelle g la fonction définie sur I par
g(x) = tan x – x.
1) Montrer que g est impaire. Lis la suite »
Maths de première sur les lois de probabilités, les variables aléatoires, calculs, exercice, espérance et écart-type, variance, comparer.
Exercice N°025 :
Exercice N°025 :
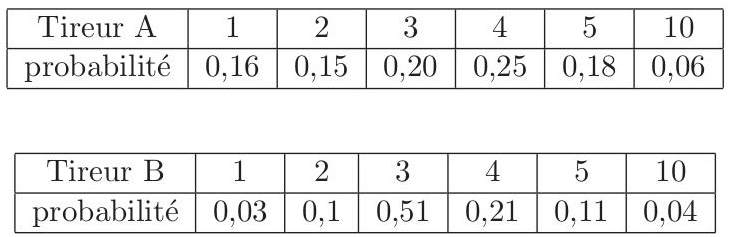
Pour une compétition internationale, le sélectionneur doit choisir entre deux tireurs à l’arc dont les performances sont définies par les lois de probabilités ci-dessous.
A chaque tir dans la cible, on associe un nombre de points. plus la flèche est proche de la cible, plus le nombre de points est élevé.
On note X et Y les variables aléatoires donnant le nombre de points obtenus à chaque tir respectivement par le tireur A et le tireur B.
1) Calculer l’espérance de chacune des deux variables aléatoires. Lis la suite »
Exercice sur les intervalles, axe, inégalité, encadrement, maths, seconde avec appartenance, crochets ouvrants et fermants.
Exercice N°644 :
Exercice N°644 :
1-2-3-4) Tracer un axe, entourer l’intervalle correspondant, puis traduisez par une (ou des) inégalité(s) la proposition indiquée.
1) x ∈ [2 ; 5], Lis la suite »
Maths de terminale : exercice sur polynôme, racine, inéquation, équation, factorisation. Discriminant, coefficients égaux, second degré.
Exercice N°238 :
Exercice N°238 :
Soit A = √(4 – √7) – √(4 + √7).
1) Calculer A2 et montrer que A2 ∈ N. Lis la suite »
Maths de seconde : exercice de fonction, courbe, équation, inéquation, étude graphique, parabole, calculs d’image et d’antécédent.
Exercice N°023 :
1-2-3) Répondre aux questions suivantes en faisant des lectures graphiques (laissez les traces de lectures sur le graphique ci-contre).
1) Donner f(0) Lis la suite »
Maths de terminale : exercice de fonction, équation, continuité, variation, nombre de solutions, limite en infini, valeurs intermédiaires.
Exercice N°248 :
On considère une fonction f définie sur [0 ; 2π] dont le tableau de variation est donné ci-dessous :
1) Montrer que l’équation f(x) = 1 admet 2 solutions sur [0 ; 2π]. Lis la suite »
Exercice de maths de terminale sur la continuité. Solution unique, tableau de signe et exercice tableau de variation terminale.
Exercice N°397 :
Exercice N°397 :
Soit f la fonction définie sur [0 ; 1] par
f(x) = −x3 + 15x2 − 75x + 5.
1) Pour tout x ∈ R, calculer f ‘ (x). Lis la suite »
Maths de terminale : exercice de suite géométrique avec algorithme, arithmétique, somme de termes, formule explicite, calculatrice, calculs.
Exercice N°230 :
Exercice N°230 :
Une entreprise fabriquant des tables en bois souhaite se développer rapidement et veut planifier l’augmentation de sa production chaque année.
En 2051, 3000 tables par an ont été fabriquées.
Deux options sont possibles pour augmenter la production :
– Plan 1: on augmente la production annuelle de 180 tables chaque année.
– Plan 2 : on augmente la production de 5 % par an.
On note un le nombre de tables fabriquées pendant l’année (2051 + n) avec le plan 1.
1) Déterminer u0. Lis la suite »
