Maths de première sur les lois de probabilités, les variables aléatoires, calculs, exercice, espérance et écart-type, variance, comparer.
Exercice N°025 :

Exercice N°025 :
Pour une compétition internationale, le sélectionneur doit choisir entre deux tireurs à l’arc dont les performances sont définies par les lois de probabilités ci-dessous.
A chaque tir dans la cible, on associe un nombre de points. plus la flèche est proche de la cible, plus le nombre de points est élevé.
On note X et Y les variables aléatoires donnant le nombre de points obtenus à chaque tir respectivement par le tireur A et le tireur B.
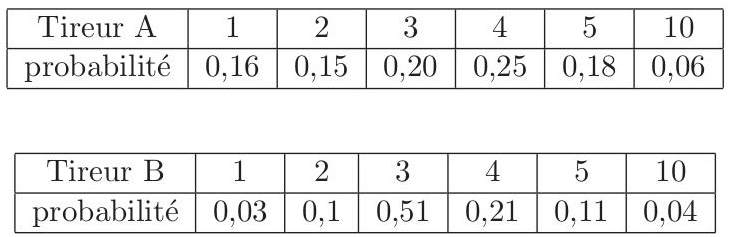
1) Calculer l’espérance de chacune des deux variables aléatoires.
2) Calculer chacun de leur écart-type.
3) Compte tenu de ces informations, quel tireur va choisir le sélectionneur ?
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, espérance, écart-type.
Exercice précédent : Fonctions – Surface de carrés et courbe dans repère – Seconde


1)1.16*1+2*0.15+3*0.20+4*0.25+5*0.18+10*0.06=
1.16+0.3+0.6+1+0.9+0.6=
4.56
E(X)=4.56
Ecart type= valeur absolue de la variance
V(x)=0.16(1-4.56)²+0.15(2-4.56)²+0.20(3-4.56)²+0.25(4-4.56)²+0.18(5-4.56)²+0.06(10-4.56)²=17.06
Ecart type =2.09437341
2)E(X)=3.55
V(X)=15.13
Ecart type= 1.5898113
Le tireur va donc choisir le tireur B car c’est un tireur plus stable.
J’attends que tu fasses la modification du calcul pour comparer..