Essaie les exercices de DS, clique ci-dessous
Maths de terminale : exercice sur le nombre de possibilités de terminale. Dénombrement, p-listes, arrangements, combinaisons, permutations.
Exercice N°715 :
Exercice N°715 :
1-2-3-4) Dans une urne se trouve 12 cartes numérotés de 1 à 12.
1-2) On tire 5 cartes successivement avec remise :
1) Combien de tirages ne comportent que des diviseurs de 12 ? Lis la suite »
Maths de terminale : exercice de limites de suites et fonctions. Rationnelles, polynômes, exponentielles, logarithme népérien, infini.
Exercice N°576 :
Exercice N°576 :
1-4) Déterminer les limites des suites suivantes lorsqu’elles existent.
1) un = n3 − 2n2 + n − 7. Lis la suite »
Maths de première : exercice d’algorithme, valeur absolue, fonction avec condition si alors, tableau et courbe, expression, repère.
Exercice N°038 :
On considère la fonction f définie sur R par
f(x) = | (1/3)x2 + 2x − 1 |.
1) Compléter le tableau de valeurs de f (ci-dessous). On donnera les résultats sous forme d’entiers ou de fractions irréductibles. Lis la suite »
Maths de première sur un exercice d’algorithme avec suite récurrente. Boucle tant que, seuil, tableau de variable, affectations, conditions.
Exercice N°037 :
On considère l’algorithme suivant :
1) Appliquer cet algorithme en complétant autant que nécessaire le tableau suivant : Lis la suite »
Exercice : Clic droit vers l’exercice
Tout le corrigé :
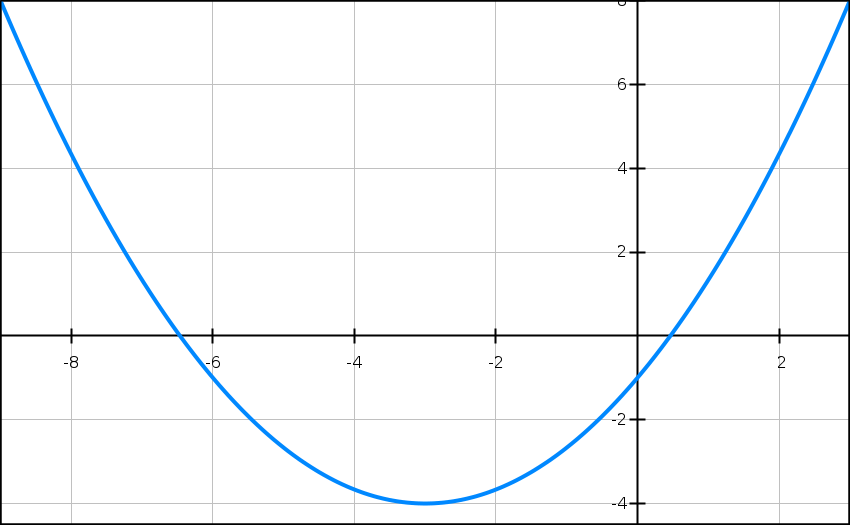
1) f(x) = x + 1 + xe-x
= x + 1 + u(x) × v(x)
avec u(x) = x
donc u'(x) = 1
avec v(x) = e-x
donc v'(x) = -e-x
f'(x) = 1 + 0 + u'(x) × v(x) + u(x) × v'(x)
= 1 + 1 × e-x + x × (-e-x)
= 1 + e-x – xe-x
f'(x) = 1 + e-x – u(x) × v(x)
avec les mêmes u(x) et v(x).
Donc f »(x) = 0 – e-x – (u'(x) × v(x) + u(x) × v'(x))
= – e-x – (1 × e-x – xe-x)
= -2e-x + xe-x
= (x – 2)e-x.
2) x-2 est négatif avant 2, puis positif après 2.
Un exponentiel est toujours strictement positif.
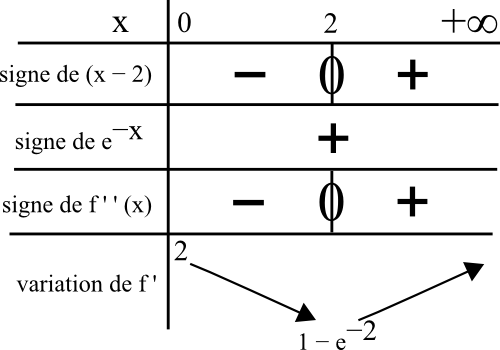
car f'(0) = 1 + e-0 – 0e-0
= 1 + 1 + 0
= 2
et f'(2) = 1 + e-2 – 2e-2
= 1 – e-2.
3) D’après le tableau de variation, on voit que le minimum de la fonction est
1 – e-2 qui est strictement positif.
Donc f'(x) > 0 sur les réels positifs.
4) f(x) = x + 1 + xe-x
lim[x → +∞] (x + 1) = +∞
Comme xe-x est positif sur R+, peu importe sa limite (0, une constante ou +∞), additionnée à la limite +∞ de (x + 1), on aura :
lim[x → +∞] f(x) = +∞
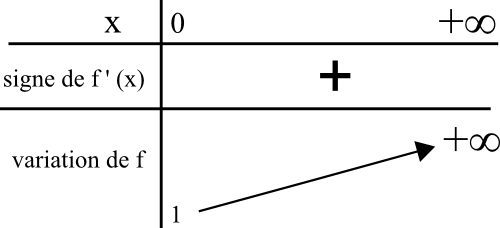
5) On sait que f'(x) est toujours positif sur R+, donc f est strictement croissante.
f(0) = 0 + 1 + 0e-0
= 1.
6) L’équation d’une tangente est :
Donc ici y = f'(1)(x – 1) + f(1).
f'(1) = 1 + e-1 – 1e-1
= 1.
f(1) = 1 + 1 + 1e-1
= 2 + e-1.
Donc y = 1(x – 1) + 2 + e-1
y = x + 1 + e-1.
7) * f est continue sur R+
* f est strictement croissante sur R+
f(0) = 1
lim[x → +∞] f(x) = +∞
* Donc 2 appartient à l’intervalle image [ 1 ; +∞ ]
soit [ f(0) ; lim[x → +∞] f(x)].
D’après le théorème des valeurs intermédiaire, l’équation f(x) = 2 admet une unique solution α sur R+.
On trouve α à l’aide de la calculatrice avec la tableur.
Tout d’abord, on part de 0 et on monte de 1 en 1 jusqu’à dépasser 2.
Donc 0 < α < 1 car on dépasse 2 dès l’abscisse x = 1.
Maintenant on va de 0.1 en 0.1 :
On dépasse 2 à partir de 0.7 donc 0.6 < α < 0.7
Maintenant on va de 0.01 en 0.01 :
On dépasse 2 à partir de 0.66 donc 0.65 < α < 0.66
Maintenant on va de 0.001 en 0.001 :
On dépasse 2 à partir de 0.659 donc 0.658 < α < 0.659
Je prends 0.659 comme valeur arrondie de α.
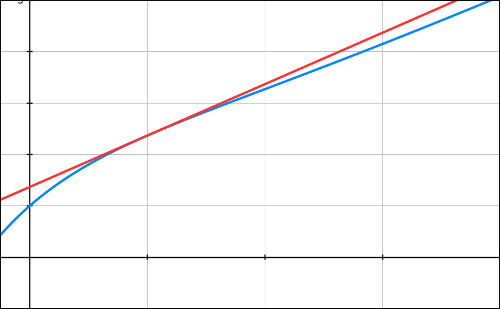
8) 
Cf est la courbe bleue et (T) la droite rouge qui est bien la tangente en 1.
Bonne compréhension,
Sylvain Jeuland
Maths de terminale, exercice de dénombrement avec combinaisons et arrangements. Nombre de cas possibles, possibilités, formules.
Exercice N°714 :
Exercice N°714 :
Au loto, on coche 6 numéros parmi les nombres de 1 à 49 de la grille.
1) Quel est le nombre de bulletins possibles ? Lis la suite »
Maths : exercice avec arrangements et p-listes de terminale. Nombre de cas possibles, nombres avec chiffres dans l’ordre, dénombrement.
Exercice N°713 :
Exercice N°713 :
On dispose de 7 couleurs pour colorier les 4 cases rectangulaires d’un drapeau (comme celui de l’Île Maurice).
1) Combien peut-on obtenir de drapeaux différents si on impose que 2 rectangles ne soient pas de la même couleur ? Lis la suite »
Exercice de maths de première d’algorithme de trigonométrie avec mesure principale, cercle, angle, conditions, boucle, entrée.
Exercice N°113 :
On considère l’algorithme ci-dessus.
1) Appliquer cet algorithme en complétant le tableau suivant : Lis la suite »
Exercice de maths de terminale sur les suites, limite, racine, cosinus. Calcul en plus infini. Polynôme, rationnelle, somme, fraction.
Exercice N°185 :
1-6) Déterminer la limite des suites suivantes :
1) rn = 2n² − 3n + 2, Lis la suite »
Maths de terminale : exercice de dénombrement avec combinaisons, p-listes. Nombres de possibilités, tirages de boules, chiffres, cartes.
Exercice N°712 :
Exercice N°712 :
1) Combien y a-t-il de numéros à 6 chiffres ? Lis la suite »
